题目内容
【题目】已知等边△ABC.
(1)如图①,P为等边△ABC外一点,且∠BPC=120°,试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想;
(2)如图②,P为等边△ABC内一点,且∠APD=120°,求证:PA+PD+PC>BD;
(3)在(2)的条件下,若∠CPD=30°,AP=4,CP=5,DP=8,求BD的长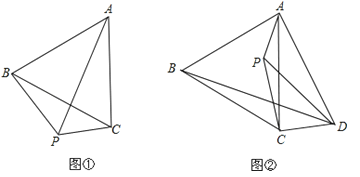
【答案】解:(1)AP=BP+PC,
证明:延长BP至E,使PE=PC,连接CE,如图1所示,
∵∠BPC=120°,
∴∠CPE=60°,
又∵PE=PC,
∴△CPE为等边三角形,
∴CP=PE=CE,∠PCE=60°,
∵△ABC为等边三角形,
∴AC=BC,∠BCA=60°,
∴∠ACB=∠PCE,
∴∠ACB+∠BCP=∠PCE+∠BCP,
即∠ACP=∠BCE,
在△ACP与△BCE中, ,
,
∴△ACP≌△BCE(SAS),
∴AP=BE,
∵BE=BP+PE,
∴AP=BP+PC;
(2)证明:延长DP到M使得PM=PA,连接AM、BM,如下图2所示,
∵∠APD=120°,PM=PA,
∴∠APM=60°,
∴△APM是等边三角形,
∴AM=AP,∠PAM=60°,
∴DM=PD+PA,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠MAP=∠BAC,
∴∠MAP﹣∠BAP=∠BAC﹣∠BAP,
即∠MAB=∠PAC,
在△AMB和△APC中,
∴△AMB≌△APC(SAS)
∴BM=PC,
∵在△BDM中,DM+BM>BD,DM=PD+PA,
∴PA+PD+PC>BD.
(3)如下图2所示,
由(2)知△AMB≌△APC,
∴MB=PC,∠AMB=∠APC,
∵∠CPD=30°,AP=4,CP=5,DP=8,∠APD=120°,∠AMP=60°,
∴MB=5,∠AMB=∠APC=∠APD+∠CPD=120°+30°=150°,
∴∠BMD=∠AMB﹣∠AMP=90°,
∵MD=MP+PD=4+8=12,MB=5,
∴BD=![]() =13,
=13,
故答案为:13.
【解析】(1)先写出线段BP、PC、AP之间的数量关系,然后根据猜想作出合适的辅助线,画出相应的图形,找出所求数量关系需要的条件即可;
(2)要证明PA+PD+PC>BD,只需要作辅助线延长DP到M使得PM=PA,连接AM、BM,画出相应的图形,根据三角形两边之和大于第三边即可证明结论;
(3)要求BD的长,根据(2)中得到的结论和题意可以得到∠BMD=90°,BM的长,MD的长,然后根据勾股定理即可求得BD的长,本题得以解决.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个