题目内容
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.

【答案】y=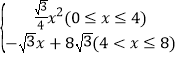 .
.
【解析】分析:作AH⊥BC于H,根据等腰三角形的性质得BH=CH,利用∠B=30°可计算出AH=2,BH=![]() ,则BC=2BH=
,则BC=2BH=![]() ,利用速度公式可得点P从B点运动到C需4s,Q点运动到C需8s,然后分类当0≤x≤4时和当4<x≤8时两种情况求中y与x之间函数关系式.
,利用速度公式可得点P从B点运动到C需4s,Q点运动到C需8s,然后分类当0≤x≤4时和当4<x≤8时两种情况求中y与x之间函数关系式.
详解:
作AH⊥BC于H,
∵AB=AC=4cm,
∴BH=CH,
∵∠B=30°,
∴AH=![]() AB=2,BH=
AB=2,BH=![]() AH=2
AH=2![]() ,
,
∴BC=2BH=4![]() ,
,
∵点P运动的速度为![]() cm/s,Q点运动的速度为1cm/s,
cm/s,Q点运动的速度为1cm/s,
∴点P从B点运动到C需4s,Q点运动到C需8s,
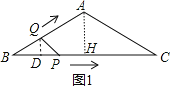
当0≤x≤4时,作QD⊥BC于D,如图1,BQ=x,BP=![]() x,
x,
在Rt△BDQ中,DQ=![]() BQ=
BQ=![]() x,
x,
∴y=![]() x
x![]() x=
x=![]() x2,
x2,
当4<x≤8时,作QD⊥BC于D,如图2,
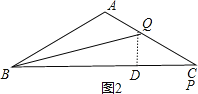
CQ=8-x,BP=4![]()
在Rt△BDQ中,DQ=![]() CQ=
CQ=![]() (8-x),
(8-x),
∴y=![]() (8-x)4
(8-x)4![]() =-
=-![]() x+8
x+8![]() ,
,
综上所述,y= .
.

练习册系列答案
相关题目