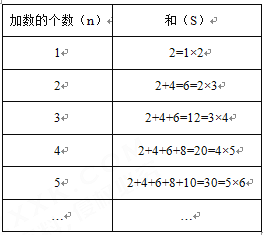
题目内容
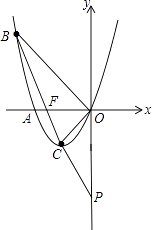
【题目】如图,已知抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C. 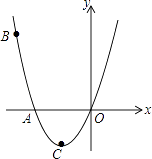
(1)求抛物线的函数解析式;
(2)连接BC交x轴于点F.试在y轴负半轴上找一点P,使得△POC∽△BOF.
【答案】
(1)解:设抛物线的解析式为y=ax2+bx+c (a≠0),
将点A(﹣2,0)、B(﹣3,3)、0(0,0),
代入可得: 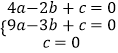
解得:a=1,b=2,c=0,
所以抛物线的解析式为y=x2+2x
(2)解:如图,
∵y=x2+2x=(x+1)2﹣1,
∴顶点C的坐标为(﹣1,﹣1).
∵B(﹣3,3),
∴tan∠BOF= ![]() =1,tan∠POC=
=1,tan∠POC= ![]() =1,
=1,
∴∠BOF=45°,∠POC=45°.
∴∠POC=∠BOF,
∴∠POC=45°=∠BOF,
设直线BC的解析式为y=kx+b(k≠0),
∵直线经过点B(﹣3,3)、C(﹣1,﹣1),
∴ ![]()
解得:k=﹣2,b=﹣3,
∴直线BC解析式为y=﹣2x﹣3,
令y=0,得x=﹣ ![]() ,
,
因此,点F(﹣ ![]() ,0),
,0),
∴OF= ![]() ,OB=
,OB= ![]() =3
=3 ![]() ,
,
OC= ![]() =
= ![]() ,
,
∵∠POC=∠BOF,
∴当 ![]() =
= ![]() 时,△POC∽△BOF,
时,△POC∽△BOF,
代入求出OP=4,
即当P点的坐标为(0,﹣4)时,△POC∽△BOF.
【解析】(1)抛物线的解析式为y=ax2+bx+c (a≠0),把A、B、C的坐标代入求出即可;(2)求出∠BOF=∠POC,求出OB、OF、OC的长,根据相似得出比例式,代入求出即可.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个