题目内容
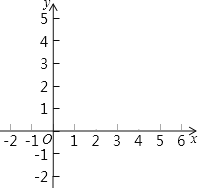
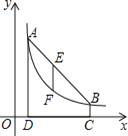
【题目】如图，点
，
在反比例函数
的图象上，
轴于点
，
轴于点
，
．
（1）求
，
的值和反比例函数的解析式；
（2）连接
，
是线段上一点，过点作
轴的垂线，交反比例函数图象于点
，若
，求点的坐标．
【答案】（1）
，
；（2）点
的坐标为
或
【解析】
（1）根据
，以及
，即
可以解出
的值，从而求出反比例函数的解析式；
（2）根据第（1）问中求出的
坐标，求出直线
的解析式为
，结合直线的解析式设出点的坐标
，而直线
平行
轴，点
在反比例函数
图象上，可以设点的坐标为
，结合已知条件
列出方程即可解出
，求得点的坐标；
解：（1）∵点
，
在反比例函数
图象上，
．
轴于点
，
轴于点
，，
，
，．
，
．
∴反比例函数的解析式为．
（2）设直线的解析式为
，
由
，
则有
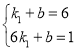，解得
，
∴直线的解析式为．
可设点的坐标为，
∵直线平行轴，点在反比例函数图象上，
∴点的坐标为．
．
，∴
，化为
．
解得
或3．
点的坐标为或．
练习册系列答案
相关题目
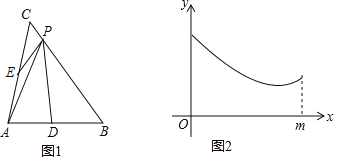
【题目】九年级某数学小组在学完《直角三角形的边角关系》这章后，决定用所学的知识设计遮阳篷（要求：遮阳篷既能最大限度地遮挡夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内）．他们制定了设计方案，并利用课余时间完成了调查和实地测量．调查和测量项目及结果如下表：
项目 | 内容 | |
课题 | 设计遮阳篷 | |
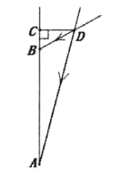
测量示意图 |
| 如图，设计了垂直于墙面AC的遮阳篷CD，AB表示窗户的高度．榆次区一年中，夏至这一天的正午时刻，太阳光线DA与遮阳篷CD的夹角∠ADC最大；冬至这一天的正午时刻，太阳光线DB与遮阳篷CD的夹角∠CDB最小． |
调查数据 |
|
|
测量数据 |
| |
… | … | |
根据上述方案及数据，求遮阳篷
的长．
（结果精确到
，参考数据：
，
，
，
，
，
）
