ЬтФПФкШн
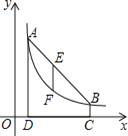
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпyЃНkx+b(kЃМ0)ЃЌОЙ§Еу(6ЃЌ0)ЃЌЧвгызјБъжсЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЪЧ9ЃЌгыКЏЪ§yЃН![]() (xЃО0)ЕФЭМЯѓGНЛгкAЃЌBСНЕуЃЎ
(xЃО0)ЕФЭМЯѓGНЛгкAЃЌBСНЕуЃЎ
(1)ЧѓжБЯпЕФБэДяЪНЃЛ
(2)КсЁЂзнзјБъЖМЪЧећЪ§ЕФЕуНазїећЕуЃЎМЧЭМЯѓGдкЕуAЁЂBжЎМфЕФВПЗжгыЯпЖЮABЮЇГЩЕФЧјгђ(ВЛКЌБпНч)ЮЊWЃЎ
ЂйЕБmЃН2ЪБЃЌжБНгаДГіЧјгђWФкЕФећЕуЕФзјБъЁЁ ЁЁЃЛ
ЂкШєЧјгђWФкЧЁга3ИіећЪ§ЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП(1)yЃНЉ![]() x+3ЃЛ(2)Ђй(3ЃЌ1)ЃЛЂк1ЁмmЃМ2ЃЎ
x+3ЃЛ(2)Ђй(3ЃЌ1)ЃЛЂк1ЁмmЃМ2ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНшжњжБЯпгыxжсЁЂyжсЕФНЛЕузјБъБэЪОГіжБЯпгызјБъжсЮЇГЩЕФШ§НЧаЮЕФСНЬѕжБНЧБпГЄЃЌРћгУУцЛ§ЪЧ9ЃЌЧѓГіжБЯпгыyжсЕФНЛЕуЮЊCЃЈ0ЃЌ3ЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЂйЯШЧѓГіЕБm=2ЪБЃЌСНКЏЪ§ЭМЯѓЕФНЛЕузјБъЃЌдйНсКЯЭМЯѓевЕНЧјгђWФкЕФећЕуЕФзјБъЃЛЂкРћгУЬиЪтжЕЗЈЧѓГіЭМЯѓОЙ§ЕуЃЈ1ЃЌ1ЃЉЁЂЃЈ2ЃЌ1ЃЉЪБЃЌЗДБШР§КЏЪ§жаmЕФжЕЃЌНсКЯЭМЯѓЕУЕНдкДЫЗЖЮЇФкЧјгђWФкећЕуга3ИіЃЌДгЖјШЗЖЈmЕФШЁжЕЗЖЮЇЮЊ1ЁмmЃМ2ЃЎ
ШчЭМЃК
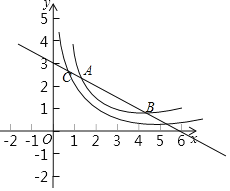
ЃЈ1ЃЉЩшжБЯпгыyжсЕФНЛЕуЮЊC(0ЃЌb)ЃЌ
ЁпжБЯпгыСНзјБъжсЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЪЧ9ЃЌ
Ёр![]() ЁС6
ЁС6![]() ЃН9ЃЌbЃНЁР3ЃЎ
ЃН9ЃЌbЃНЁР3ЃЎ
ЁпkЃМ0ЃЌ
ЁрbЃН3ЃЌ
ЁпжБЯпyЃНkx+bОЙ§Еу(6ЃЌ0)КЭ(0ЃЌ3)ЃЌ
ЁржБЯпЕФБэДяЪНЮЊyЃНЉ![]() x+3ЃЛ
x+3ЃЛ
ЃЈ2ЃЉЂйЕБmЃН2ЪБЃЌСНКЏЪ§ЭМЯѓЕФНЛЕузјБъЮЊЗНГЬзщ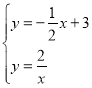 ЕФНтЃЌ
ЕФНтЃЌ
ЁрA(3Љ![]() ЃЌ
ЃЌ![]() )ЃЌB(3+
)ЃЌB(3+![]() ЃЌ
ЃЌ![]() )ЃЌЙлВьЭМЯѓПЩЕУЧјгђWФкЕФећЕуЕФзјБъЮЊ(3ЃЌ1)ЃЛ
)ЃЌЙлВьЭМЯѓПЩЕУЧјгђWФкЕФећЕуЕФзјБъЮЊ(3ЃЌ1)ЃЛ
ЂкЕБyЃН![]() ЭМЯѓОЙ§Еу(1ЃЌ1)ЪБЃЌдђ mЃН1ЃЌ
ЭМЯѓОЙ§Еу(1ЃЌ1)ЪБЃЌдђ mЃН1ЃЌ
ЕБyЃН![]() ЭМЯѓОЙ§Еу(2ЃЌ1)ЪБЃЌдђ mЃН2ЃЌ
ЭМЯѓОЙ§Еу(2ЃЌ1)ЪБЃЌдђ mЃН2ЃЌ
ЁрЙлВьЭМЯѓПЩЕУЧјгђWФкЕФећЕуга3ИіЪБ1ЁмmЃМ2ЃЎ