题目内容
【题目】已知直线![]() 或
或![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,
两点,![]() ,则
,则![]() 的值为__________.
的值为__________.
【答案】0或4或-4
【解析】
首先对一次函数进行分类讨论,由于反比例函数![]() 的图象在第一、三象限,所以①
的图象在第一、三象限,所以①![]() 与反比例函数
与反比例函数![]() 交于
交于![]() ,
,![]() 两点,此时根据
两点,此时根据![]() ,以及直线
,以及直线![]() 与坐标轴的夹角为
与坐标轴的夹角为![]() ,可以求出
,可以求出![]() 两点的坐标为
两点的坐标为![]() ,
,![]() ,代入直线
,代入直线![]() 即可解出
即可解出![]() ;②
;②![]() 与反比例函数
与反比例函数![]() 交于
交于![]() ,
,![]() 两点,此时还应再分两种情况,i:
两点,此时还应再分两种情况,i:![]() ,设出
,设出![]() 的横坐标为
的横坐标为![]() ,则纵坐标为
,则纵坐标为![]() ,利用反比例函数的性质列出方程
,利用反比例函数的性质列出方程![]() ,解出
,解出![]() 即可求出
即可求出![]() 的值;ii:
的值;ii:![]() ,和上面同样的方法即可求解;
,和上面同样的方法即可求解;
因为直线![]() 或
或![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,①由于反比例函数
两点,①由于反比例函数![]() 的图象在第一、三象限,当
的图象在第一、三象限,当![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且
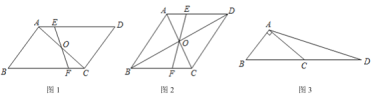
两点,且![]() 时(如图1),因为反比例函数
时(如图1),因为反比例函数![]() 的图象的两支最接近的两点
的图象的两支最接近的两点![]() 与
与![]() 之间的距离为4,此时
之间的距离为4,此时![]() ;②当直线
;②当直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
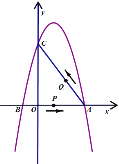
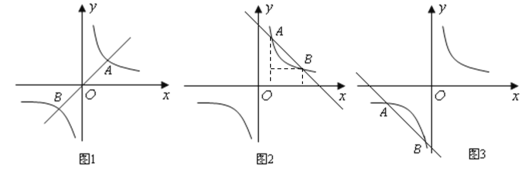
,![]() 两点时,应分两种情况:一是在图2中,
两点时,应分两种情况:一是在图2中,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,则纵坐标为
,则纵坐标为![]() ,则有
,则有![]() ,解得
,解得![]() ,则有
,则有![]() 过点
过点![]() ,代入解析式中可得
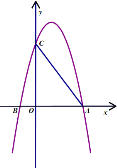
,代入解析式中可得![]() ;同理,在图3中,可求得
;同理,在图3中,可求得![]() .
.
故答案是:0或4或-4

 导学全程练创优训练系列答案
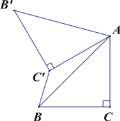
导学全程练创优训练系列答案【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 延长线上的定点,
延长线上的定点,![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
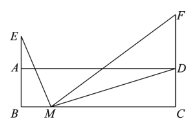
小东根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小东探究的过程,请补充完整:
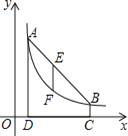
(1)对于点![]() 在
在![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
在![]() 的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的两个函数的图象;
中,画出(1)中所确定的两个函数的图象;
(3)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的长度约为________
的长度约为________![]() .
.

【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?