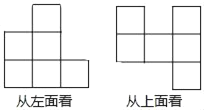
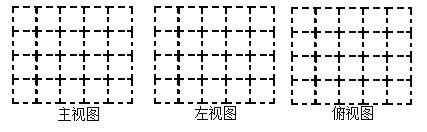
��Ŀ����
����Ŀ��С��Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�ƣ����۹����з��֣�ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����y=��10x+500�������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�60%��
��1����С��ÿ�»������Ϊw��Ԫ������ÿ�»������w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��2�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������ÿ�µ���������Ƕ��٣�
��3�����С����Ҫÿ�»�õ�������2000Ԫ����ôС��ÿ�µijɱ�������Ҫ����Ԫ�����ɱ�=��������������
���𰸡���1![]() ��20��x��32������2�������۵��۶�Ϊ32Ԫʱ��ÿ�¿ɻ������������������2160Ԫ����3��3600��
��20��x��32������2�������۵��۶�Ϊ32Ԫʱ��ÿ�¿ɻ������������������2160Ԫ����3��3600��
�������������������1��������ã�ÿ�������������۵���֮��Ĺ�ϵ�ɽ��ƿ���һ�κ���������=�����������ۣ������������Ӷ��г���ϵʽ��
��2������ȷ�����κ����ĶԳ��ᣬȻ�������������ȷ��������ɣ�
��3�����������ߵ����ʺ�ͼ�����ÿ�µijɱ���
�����������1�������⣬�ã�w=��x��20��y=��x��20������10x+500��=![]() ����
����![]() ��20��x��32����
��20��x��32����
��2�����ں���![]() ��ͼ��ĶԳ�����ֱ��x=
��ͼ��ĶԳ�����ֱ��x=![]() =35��
=35��
����a=��10��0�������߿������£�����20��x��32ʱ��W����X���������������x=32ʱ��W=2160
�𣺵����۵��۶�Ϊ32Ԫʱ��ÿ�¿ɻ������������������2160Ԫ��
��3��ȡW=2000�ã�![]()
��������̵ã� ![]() =30��
=30�� ![]() =40��
=40��
��a=��10��0�������߿������£�����30��x��40ʱ��w��2000��
��20��x��32������30��x��32ʱ��w��2000��
��ÿ�µijɱ�ΪP��Ԫ���������⣬�ã�P=20����10x+500��=��200x+10000
��k=��200��0����P��x���������С������x=32ʱ��P��ֵ��С��P��Сֵ=3600��
����Ҫÿ�»�õ�������2000Ԫ��С��ÿ�µijɱ�����Ϊ3600Ԫ��

 ��У����ϵ�д�
��У����ϵ�д�