Question

【题目】如图所示，△ABC中，∠C=90°，BC=8cm，AC：AB=3：5，点P从点B出发沿BC向点C以2cm/s的速度移动，点Q从点C出发沿CA向点A以1cm/s的速度移动，如果P、Q分别从B、C同时出发：

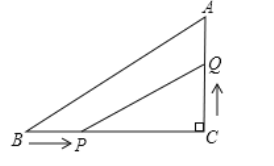
（1）经过多少秒后，△CPQ的面积为8cm？

（2）经过多少秒时，以C、P、Q为顶点的三角形恰与△ABC相似？

Answer 1

【答案】（1）不论经过多少秒后，△CPQ的面积都不能为8cm2；（2）2.4秒或秒

【解析】

（1）设AC=3x，AB=5x，根据勾股定理列出方程即可求出AC和AB，设经过t秒后，△CPQ的面积为8cm2，然后用t表示出PC和CQ，根据三角形的面积列方程即可求出结论；

（2）设经过x秒时，以C、P、Q为顶点的三角形恰与△ABC相似，根据有两组对应边成比例及其夹角相等的两个三角形相似，列出比例式，即可求出结论．

解：设AC=3x，AB=5x，由勾股定理得：AB2=AC2+BC2，

∴（3x）2+82=（5x）2，

解得：x=2，

∴AC=6，AB=10，

设经过t秒后，△CPQ的面积为8cm2， PC=8-2t，CQ=t，

PC×CQ=8即×（8-2t）×t=8

解得：此方程无解，

答：不论经过多少秒后，△CPQ的面积都不能为8cm2．

（2）解：设经过x秒时，以C、P、Q为顶点的三角形恰与△ABC相似，

∵∠C=∠C=90°，

∴要使以C、P、Q为顶点的三角形恰与△ABC相似，具备或=就行，代入得：或，

解得：x=或x=，

答：经过秒或秒时，以C、P、Q为顶点的三角形恰与△ABC相似．