Question

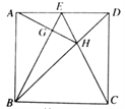
【题目】如图，正方形ABCD的边长为6，点E是AD的中点，连接BE、CE，CE与BD相交于点H，连接AH，交BE于点G，则GH的长为__________．

Answer 1

【答案】

【解析】

根据正方形的性质证明△ABE≌△DCE，△CDH≌△ADH，得出∠ABE＝∠DAH，进而得出∠AGE＝90°，根据勾股定理求出BE，BD的长，利用三角形的面积公式得出AG的长，根据△EDH∽△CBH，可求出BH的长，最后利用勾股定理求出GH的长．

∵正方形ABCD的边长为6，点E是AD的中点，

∴AD＝CD＝BC＝AB＝6，AE＝3，∠BAE＝∠BCD＝90°，AD∥BC，

∴△ABE≌△DCE，

∴∠ABE＝∠DCE，

∵DH＝DH，∠CDH＝∠ADH，CD＝AD，

∴△CDH≌△ADH，

∴∠DCE＝∠DAH，

∴∠ABE＝∠DAH，

∵∠ABE +∠AEG＝90°，

∴∠DAH +∠AEG＝90°，

∴∠AGE＝90°，

∵由勾股定理知，，，

∵，

∴，

∴由勾股定理知，，

∵AD∥BC,∴△EDH∽△CBH，

∴，

∴，

∴由勾股定理知，，

故答案为：．