Question

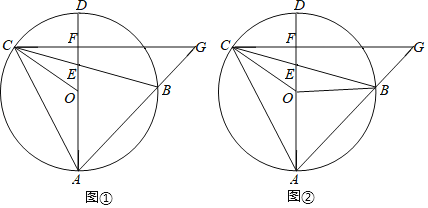
【题目】如图①，已知△ABC内接于⊙O，BC交直径AD于点E，过点C作AD的垂线交AB的延长线于点G，垂足为F，连接OC．

（1）求证：∠ACB＝∠G；

（2）如图②，连接OB，若AB＝AE，，求的值．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）连接CD，根据圆周角定理和垂直的定义可得结论；
（2）过O作OG⊥AB于G，设CF＝x，则AF＝2x．通过证得△COF≌△OAN（AAS），得到AN＝OF，ON＝CF＝x．设OF＝a，则OA＝OC＝2xa，根据勾股定理列方程得：（2xa）2＝x2＋a2，则a＝x，代入面积公式可得结论．

（1）证明：如图①，连接CD，

∵AD是⊙O的直径，

∴∠ACD＝90°．

∴∠ACB+∠BCD＝90°．

∵AD⊥CG，

∴∠AFG＝∠G+∠BAD＝90°．

∵∠BAD＝∠BCD，

∴∠ACB＝∠G；

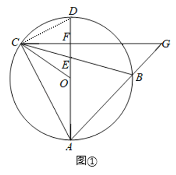
（2）解：如图②，过点O作ON⊥AB于点N，连接CD，设CF＝x，

∵tan∠CAF＝＝，

∴AF＝2x．

∵AB＝AE，

∴∠ABE＝∠AEB，

∵∠ABC＝∠G+∠BCG，∠AEB＝∠ACB+∠DAC，

∵∠ACB＝∠G；

∴∠BCG＝∠DAC，

∴＝，

∵AD⊥CH，

∴＝，

∴2＝，

∴2∠CAD＝∠BAD，

∵∠COF＝2∠CAD，

∴∠COF＝∠BAD，

∵OC＝OA，∠OFC＝∠ONA＝90°，

∴△COF≌△OAN（AAS）．

∴AN＝OF，ON＝CF＝x．

设OF＝a，则OA＝OC＝2x﹣a，在Rt△COF中，CO2＝CF2+OF2，

∴（2x﹣a）2＝x2+a2．

∴a＝x．

∴OF＝AN＝x．

∵OA＝OB，ON⊥AB，

∴AB＝2AN＝x．

∴．