题目内容
【题目】如图,A(1,0),B(4,0),M(5,3).动点P从点A出发,沿x轴以每秒1个单位长的速度向右移动,且过点P的直线l:y=-x+b也随之移动.设移动时间为t秒.
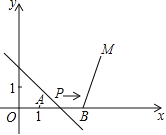
(1)当t=1时,求l的解析式;
(2)若l与线段BM有公共点,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在y轴上.如不存在,请说明理由.
【答案】(1)y=-x+2 (2)3≤t≤7 (3)t为2时,点M关于l的对称点落在y轴上.
【解析】
(1)利用一次函数图象上点的坐标特征,求出一次函数的解析式;
(2)分别求出直线l经过点B、点M时的t值,即可得到t的取值范围;
(3)找出点M关于直线l在y轴上的对称点C,如解答图所示.求出点C的坐标,然后求出MC中点坐标,最后求出t的值.
解:(1)直线y=-x+b交x轴于点P(1+t,0),
由题意,得b>0,t≥0,.
当t=1时,-2+b=0,解得b=2,
故y=-x+2.
(2)当直线y=-x+b过点B(4,0)时,
0=-4+b,
解得:b=4,
0=-(1+t)+4,
解得t=3.
当直线y=-x+b过点M(5,3)时,
3=-5+b,
解得:b=8,
0=-(1+t)+8,
解得t=7.
故若l与线段BM有公共点,t的取值范围是:3≤t≤7.
(3)如图,

过点M作MC⊥直线l,交y轴于点C,交直线l于点D,则点C为点M在坐标轴上的对称点.
设直线MC的解析式为y=x+m,则
3=5+m,解得m=-2,
故直线MC的解析式为y=x-2.
当x=0时,y=0-2=-2,
则C点坐标为(0,-2),
∵(0+5)÷2=2.5,
(3-2)÷2=0.5,
∴D点坐标为(2.5,0.5),
当直线y=-x+b过点D(2.5,0.5)时,
0.5=-2.5+b,
解得:b=3,
0=-(1+t)+3,
解得t=2.
∴t为2时,点M关于l的对称点落在y轴上.

 阅读快车系列答案
阅读快车系列答案