Question

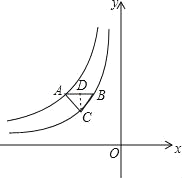
【题目】如图，△ABC是等腰直角三角形，∠ACB＝90°，点A在反比例函数y＝﹣的图象上，点B、C都在反比例函数y＝﹣的图象上，AB∥x轴，则点A的坐标为（ ）

A.(﹣，2)B.(﹣，)C.(﹣，)D.(﹣2，)

Answer 1

【答案】B

【解析】

作CD⊥AB于D，设B（t，﹣），根据AB∥x轴，即可表示A（2t，﹣），根据等腰直角三角形的性质和反比例函数的性质列方程求出t的值，即可得到点A的坐标．

解：作CD⊥AB于D，如图，

设B（t，﹣），

∵AB∥x轴，

∴A点的纵坐标为﹣，

∴A（2t，﹣），

∵△ABC是等腰直角三角形，CD⊥AB，

∴AD＝BD，CD＝AB，CD∥y轴，

∴D点坐标为（t，﹣），

∴C点的横坐标为t，

∵点C在反比例函数y＝﹣的图象上，

∴C（t，﹣），

∵AB＝t﹣2t＝﹣t，CD＝﹣+，

∴﹣+＝×（﹣t），

解得t＝﹣或t＝（舍去），

∴A（﹣，）．

故选：B．