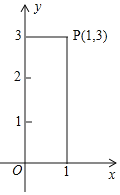题目内容
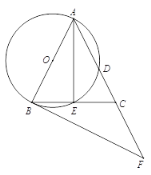
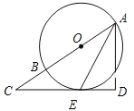
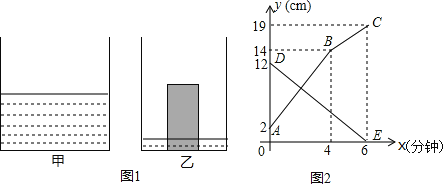
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块放于其中(圆柱形铁块的下底面完全落在水槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(1)注水多长时间时,甲、乙两个水槽中的水的深度相同?
(2)若乙槽底面积为42平方厘米(壁厚不计),求乙槽中铁块的体积;
(3)若乙槽中铁块的体积为168立方厘米(壁厚不计),求甲槽底面积.
【答案】(1)2分钟;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设线段AB、DE的解析式分别为:y1=k1x+b1,y2=k2x+b2,利用待定系数法求出y1与y2的函数表达式,最后利用![]() 进行求解;
进行求解;
(2)设铁块的底面积为![]() ,则乙水槽中不放铁块每分钟的进水量为
,则乙水槽中不放铁块每分钟的进水量为![]() ,放了铁块后每分钟的进水量为
,放了铁块后每分钟的进水量为![]() ,列出方程进行求解,进而得出结论;
,列出方程进行求解,进而得出结论;
(3)设甲槽的底面积为![]() ,乙槽的底面积为
,乙槽的底面积为![]() ,根据前4分钟和后2分钟甲槽中流出的水的体积和乙槽中流入的水的体积分别相等,列二元一次方程组,求解即可.
,根据前4分钟和后2分钟甲槽中流出的水的体积和乙槽中流入的水的体积分别相等,列二元一次方程组,求解即可.
解:(1)设线段AB、DE的解析式分别为:y1=k1x+b1,y2=k2x+b2,
∵AB经过点(0,2)和(4,14),DE经过(0,12)和(6,0),
∴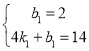 ,
,
解得,![]() ,
,
∴可得线段![]() 解析式为
解析式为![]() ;
;
∴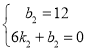 ,
,
解得,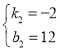 ,
,
∴线段DE解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
解得![]() ,
,
∴当2分钟时两个水槽中的水的深度相同;
(2)由图象知:当水槽中没有没过铁块时4分钟水面上升了12cm,即1分钟上升3cm,当水面没过铁块时,2分钟上升了5cm,即1分钟上升2.5cm,
设铁块的底面积为![]() ,则乙水槽中不放铁块每分钟的进水量为:
,则乙水槽中不放铁块每分钟的进水量为:![]() ,放了铁块后每分钟的进水量为
,放了铁块后每分钟的进水量为![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 铁块的体积为:
铁块的体积为:![]() .
.
(3)![]() 铁块的体积为
铁块的体积为![]() ,
,
![]() 铁块的底面积为
铁块的底面积为![]() ,
,
可设甲槽的底面积为![]() ,乙槽的底面积为
,乙槽的底面积为![]() ,
,
根据前4分钟和后2分钟甲槽中流出的水的体积和乙槽中流入的水的体积分别相等,列二元一次方程组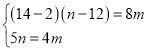 ,
,
解得:![]() ,
,
所以甲槽底面积为![]() .
.

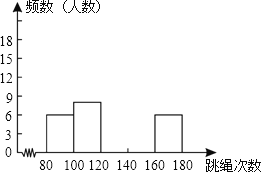
【题目】为了进一步了解某校九年级1000名学生的身体素质情况,体育老师对该校九年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,试估计该年级学生不合格的人数大约有多少人?
【题目】某校九年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人跳100个以上(含100个)为优秀.下表是甲班和乙班5名学生的比赛数据(每跳1个记1分,单位:分):
1号 | 2号 | 3号 | 4号 | 5号 | 总计 | |
甲班 | 100 | 98 | 110 | 89 | m | 500 |
乙班 | 89 | n | 95 | 119 | 97 | 500 |
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,来确定冠军.请你回答下列问题:
(1)上表中,m=______,n=_____;
(2)若从两班参赛的这10名同学中,随机选择1人,求其成绩为优秀的概率;
(3)试从两班比赛成绩的优秀率、中位数和极差三个方面加以分析,判断冠军应该属于哪个班级?并简要说明理由.