ΧβΡΩΡΎ»ί
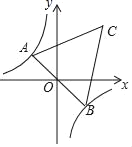
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏyΘΫ©¹x2+bx+c”κx÷αΫΜ”ΎAΘ®©¹1Θ§0Θ©Θ§BΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ®0Θ§3Θ©Θ§Ής÷±œΏBCΘ°Ε·ΒψP‘Ύx÷α…œ‘ΥΕ·Θ§ΙΐΒψPΉςPMΓΆx÷αΘ§ΫΜ≈ΉΈοœΏ”ΎΒψMΘ§ΫΜ÷±œΏBC”ΎΒψNΘ§…ηΒψPΒΡΚαΉχ±ξΈΣmΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±ΒψP‘ΎœΏΕΈOB…œ‘ΥΕ· ±Θ§«σœΏΕΈMNΒΡΉν¥σ÷ΒΘΜ
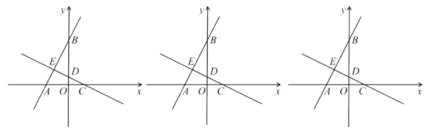
Θ®3Θ© «Ζώ¥φ‘ΎΒψPΘ§ ΙΒΟ“‘ΒψCΓΔOΓΔMΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωmΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
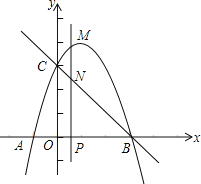
ΓΨ¥πΑΗΓΩ(1)yΘΫ©¹x2+2x+3ΘΜ(2)œΏΕΈMNΉν¥σ÷ΒΈΣ![]() ΘΜ(3)¥φ‘ΎΒψPΘ§ ΙΒΟ“‘ΒψCΓΔOΓΔMΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§¥Υ ±mΒΡ÷ΒΈΣ
ΘΜ(3)¥φ‘ΎΒψPΘ§ ΙΒΟ“‘ΒψCΓΔOΓΔMΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§¥Υ ±mΒΡ÷ΒΈΣ![]() Μρ
Μρ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
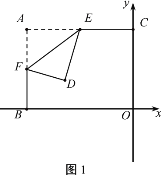
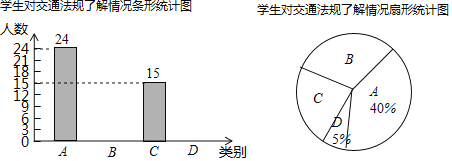
Θ®1Θ©ΗυΨίΒψAΓΔCΒΡΉχ±ξΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©”…Εΰ¥ΈΚ· ΐΆΦœσ…œΒψΒΡΉχ±ξΧΊ’ςΩ…’“≥ωΒψBΒΡΉχ±ξΘ§ΗυΨίΒψBΓΔCΒΡΉχ±ξΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Ω…«σ≥ω÷±œΏBCΒΡΫβΈω ΫΘ§…ηΒψPΒΡΉχ±ξΈΣΘ®mΘ§0Θ©Θ®0ΓήmΓή3Θ©Θ§ΒψMΒΡΉχ±ξΈΣΘ®mΘ§©¹m2+2m+3Θ©Θ§ΒψNΒΡΉχ±ξΈΣΘ®mΘ§©¹m+3Θ©Θ§”…¥ΥΦ¥Ω…ΒΟ≥ωMNΘΫ©¹m2+3mΘ§άϊ”Ο≈δΖΫΖ®Φ¥Ω…«σ≥ωœΏΕΈMNΒΡΉν¥σ÷ΒΘΜ
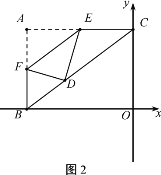
Θ®3Θ©ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ Ω…ΒΟ≥ωMNΘΫOCΘ§Ζ÷mΘΦ0ΜρmΘΨ3“‘ΦΑ0ΓήmΓή3ΝΫ÷÷«ιΩωΘ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎmΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
(1)ΫΪA(©¹1Θ§0)ΓΔC(0Θ§3)¥ζ»κyΘΫ©¹x2+bx+c÷–Θ§
![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() ,
,
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣyΘΫ©¹x2+2x+3Θ°
(2)Β±yΘΫ©¹x2+2x+3ΘΫ0 ±Θ§x1ΘΫ©¹1Θ§x2ΘΫ3Θ§
ΓύΒψBΒΡΉχ±ξΈΣ(3Θ§0)Θ°
…η÷±œΏBCΒΡΫβΈω ΫΈΣyΘΫkx+b(kΓΌ0)Θ§
ΫΪB(3Θ§0)ΓΔC(0Θ§3)¥ζ»κyΘΫkx+b÷–Θ§
![]() ,Θ§ΫβΒΟΘΚ
,Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ÷±œΏBCΒΡΫβΈω ΫΈΣyΘΫ©¹x+3Θ°
…ηΒψPΒΡΉχ±ξΈΣ(mΘ§0)(0ΓήmΓή3)Θ§ΒψMΒΡΉχ±ξΈΣ(mΘ§©¹m2+2m+3)Θ§
ΒψNΒΡΉχ±ξΈΣ(mΘ§©¹m+3)Θ§
ΓύMNΘΫ©¹m2+2m+3©¹(©¹m+3)ΘΫ©¹m2+3mΘΫ©¹(m©¹![]() )2+
)2+![]() Θ§
Θ§
ΓύΒ±mΘΫ![]() Θ§œΏΕΈMN»ΓΉν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ
Θ§œΏΕΈMN»ΓΉν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ![]() Θ°
Θ°
(3)ÿMNøCOȧ
ΓύΒ±MNΘΫCO ±Θ§“‘ΒψCΓΔOΓΔMΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ°
ΓΏΒψO(0Θ§0)ΓΔC(0Θ§3)Θ§
ΓύOCΘΫ3Θ§
Γύ|©¹m2+3m|ΘΫ3Θ§
Β±mΘΦ0ΜρmΘΨ3 ±Θ§”–m2©¹3mΘΫ3Θ§
ΫβΒΟΘΚm1ΘΫ![]() Θ§m2ΘΫ
Θ§m2ΘΫ![]() ΘΜ
ΘΜ
Β±0ΓήmΓή3 ±Θ§”–©¹m2+3mΘΫ3Θ§
ΓΏΓςΘΫ(©¹3)2©¹4ΓΝ1ΓΝ3ΘΫ©¹3ΘΦ0Θ§
Γύ¥Υ ±ΖΫ≥ΧΈόΫβΘ°
Ήέ…œΥυ ωΘΚ¥φ‘ΎΒψPΘ§ ΙΒΟ“‘ΒψCΓΔOΓΔMΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§¥Υ ±mΒΡ÷ΒΈΣ![]() Μρ
Μρ![]() Θ°
Θ°