题目内容
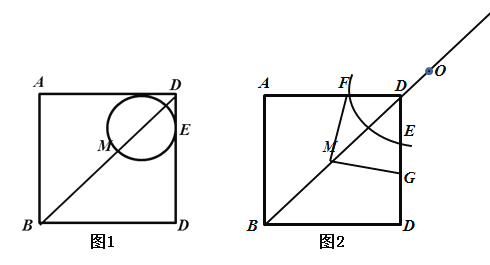
【题目】已知正方形ABCD的边长为2，中心为M，⊙O的半径为r，圆心O在射线BD上运动，⊙O与边CD仅有一个公共点E.
（1）如图1，若圆心O在线段MD上，点M在⊙O上，OM=DE，判断直线AD与⊙O的位置关系，并说明理由；
（2）如图2，⊙O与边AD交于点F，连接MF，过点M作MF的垂线与边CD交于点G，若
，设点O与点M之间的距离为
,EG=
,当
时，求
的函数解析式.
【答案】（1）相切，证明详见解析；（2）
.
【解析】
（1）过O作OF⊥AD于F，连接OE,可证△ODF≌△ODE，可得OF=OE,根据相切判定即可得出：AD与
相切；
（2）连接MC，可证
，可得DF=CG，过点E作EP⊥BD于P，过点F作FH⊥BD于H设DP=a，DH=b，由于△DHF与△DPE都是等腰直角三角形，设EP=DP=a，FH=DH=b,利用勾股定理：可列出方程组
解得a=b，可得
， 
.由于
可得
，由
可得OD=a， 由OD=OM-DM，可得
， 代入2DF+y=2可得
，整理得y与x的函数解析式,由DF≤1， EG≥0，可得x的取值范围，即可求解问题.
解：（1）直线AD与⊙O相切，理由如下：
过O作OF⊥AD于F，连接OE
∴∠OFD=90°
在正方形ABCD中，BD平分∠ADE，∠ADE=90°
∴∠FDO=∠EDO=45°
∵与CD仅有一个公共点E
∴CD与相切
∴OE⊥DC，OE为半径
∴∠OED=90°
又∵OD=OD
∴△ODF≌△ODE
∴OF=OE
∵OF⊥AD、OF=OE
∴AD与相切
（2）连接MC
在正方形ABCD中，∠BCD=90°，∠ADB =45°
∵∠BCD=90°，M为正方形的中心
∴MC=MD=
，∠ADB=∠DCM=45°
∵FM⊥MG，即∠FMG=90°
且在正方形ABCD中，∠DMC=90°
∴∠FMD+∠DMG=∠DMG+∠CMG
∴∠FMD=∠CMG
∴
∴DF=CG
过点E作EP⊥BD于P，过点F作FH⊥BD于H
设DP=a，DH=b
∵∠FDM=∠EDM=45°
∴△DHF与△DPE都是等腰直角三角形
∴EP=DP=a，FH=DH=b
∵
，且由（1）得
∴点O在正方形ABCD外
∴OP=OD+DP，OH=OD+DH
在Rt△OPE与Rt△OHF中
得：（a-b）(OD+a+b)=0
∴a-b=0或OD+a+b=0
∵OD+a+b>0
∴a-b=0
∴a=b
即点P与点H重合，也即EF⊥BD，垂足为P（或H）
∵DP=a，DH=b
∵在Rt△DPE中，
在Rt△DHF中，
∴DF=DE
∵CD=DE+EG+CG=2，即2DF+EG=2
∴2DF+y=2
∵在Rt△DPF中，
，且
∴
在Rt△OPE与Rt△OHF中
∴
∴OD+a=2a
∴OD=a
又因为 OD=OM-DM，即
∴
又因为 2DF+y=2
∴
∴
∴
∵DF≤1，且2DF+EG=2
∴EG≥0，即y≥0
∴
∴
∴y与x的函数解析式为
