题目内容
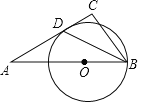
【题目】如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为![]() 的中点,过点D作DE∥AC,交BC的延长线于点E.
的中点,过点D作DE∥AC,交BC的延长线于点E.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若CE=![]() ,AB=6,求⊙O的半径.
,AB=6,求⊙O的半径.
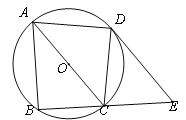
【答案】(1)DE与⊙O相切;理由见解析;(2)4.
【解析】
(1)连接OD,由D为![]() 的中点,得到
的中点,得到![]() ,进而得到AD=CD,根据平行线的性质得到∠DOA=∠ODE=90°,求得OD⊥DE,于是得到结论;
,进而得到AD=CD,根据平行线的性质得到∠DOA=∠ODE=90°,求得OD⊥DE,于是得到结论;
(2)连接BD,根据四边形对角互补得到∠DAB=∠DCE,由![]() 得到∠DAC=∠DCA=45°,求得△ABD∽△CDE,根据相似三角形的性质即可得到结论.
得到∠DAC=∠DCA=45°,求得△ABD∽△CDE,根据相似三角形的性质即可得到结论.
(1)解:DE与⊙O相切
证:连接OD,在⊙O中
∵D为![]() 的中点
的中点
∴![]()
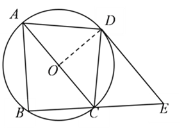
∴AD=DC
∵AD=DC,点O是AC的中点
∴OD⊥AC
∴∠DOA=∠DOC=90°
∵DE∥AC
∴∠DOA=∠ODE=90°
∵∠ODE=90°
∴OD⊥DE
∵OD⊥DE,DE经过半径OD的外端点D
∴DE与⊙O相切.
(2)解:连接BD
∵四边形ABCD是⊙O的内接四边形
∴∠DAB+∠DCB=180°
又∵∠DCE+∠DCB=180°
∴∠DAB=∠DCE
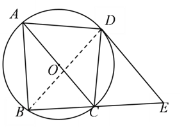
∵AC为⊙O的直径,点D、B在⊙O上,
∴∠ADC=∠ABC=90°
∵![]() ,
,
∴∠ABD=∠CBD=45°
∵AD=DC,∠ADC=90°
∴∠DAC=∠DCA=45°
∵DE∥AC
∴∠DCA=∠CDE=45°
在△ABD和△CDE中
∵∠DAB=∠DCE,∠ABD=∠CDE=45°
∴△ABD∽△CDE
∴![]() =
=![]()
∴![]() =
=![]()
∴AD=DC=4![]() , CE=
, CE=![]() ,AB=6,
,AB=6,
在Rt△ADC中,∠ADC=90°,AD=DC=4![]() ,
,
∴AC=![]() =8
=8
∴⊙O的半径为4.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.