Question

【题目】如图，在平面直角坐标系xOy中，P是直线y＝2上的一个动点，⊙P的半径为1，直线OQ切⊙P于点Q，则线段OQ取最小值时，Q点的坐标为_____．

Answer 1

【答案】（，）．

【解析】

连接PQ、OP，如图，根据切线的性质得PQ⊥OQ，再利用勾股定理得到OQ=，利用垂线段最短，当OP最小时，OQ最小，然后求出OP的最小值，得到OQ的最小值，于是得到结论．

连接PQ、OP，如图，

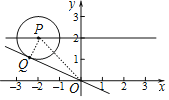
∵直线OQ切⊙P于点Q，

∴PQ⊥OQ，

在Rt△OPQ中，OQ＝＝，

当OP最小时，OQ最小，

当OP⊥直线y＝2时，OP有最小值2，

∴OQ的最小值为＝．

设点Q的横坐标为a，

∴S△OPQ＝×＝×2×|a，

∴a＝，

∴Q点的纵坐标＝＝，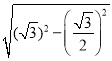

∴Q点的坐标为（，），

故答案为（，）．