题目内容
【题目】现有一次函数y＝mx+n和二次函数y＝mx2+nx+1，其中m≠0，
（1）若二次函数y＝mx2+nx+1经过点（2，0），（3，1），试分别求出两个函数的解析式．
（2）若一次函数y＝mx+n经过点（2，0），且图象经过第一、三象限．二次函数y＝mx2+nx+1经过点（a，y1）和（a+1，y2），且y1＞y2，请求出a的取值范围．
（3）若二次函数y＝mx2+nx+1的顶点坐标为A（h，k）（h≠0），同时二次函数y＝x2+x+1也经过A点，已知﹣1＜h＜1，请求出m的取值范围．
【答案】（1）y＝x﹣2，y=
x2+
+1；（2）a＜
；（3）m＜﹣2或m＞0．
【解析】
（1）直接将点代入函数解析式，用待定系数法即可求解函数解析式；
（2）点（2，0）代入一次函数解析式，得到n＝2m，利用m与n的关系能求出二次函数对称轴x＝1，由一次函数经过一、三象限可得m＞0，确定二次函数开口向上，此时当 y1＞y2，只需让a到对称轴的距离比a＋1到对称轴的距离大即可求a的范围．
（3）将A（h，k）分别代入两个二次函数解析式，再结合对称抽得h＝
，将得到的三个关系联立即可得到
，再由题中已知1＜h＜1，利用h的范围求出m的范围．
（1）将点（2，0），（3，1），代入一次函数y＝mx+n中，
，
解得
，
∴一次函数的解析式是y＝x﹣2，
再将点（2，0），（3，1），代入二次函数y＝mx2+nx+1，
，
解得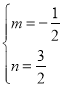
，
∴二次函数的解析式是
．
（2）∵一次函数y＝mx+n经过点（2，0），
∴n＝﹣2m，
∵二次函数y＝mx2+nx+1的对称轴是x＝，
∴对称轴为x＝1，
又∵一次函数y＝mx+n图象经过第一、三象限，
∴m＞0，
∵y1＞y2，
∴1﹣a＞1+a﹣1，
∴a＜．
（3）∵y＝mx2+nx+1的顶点坐标为A（h，k），
∴k＝mh2+nh+1，且h＝，
又∵二次函数y＝x2+x+1也经过A点，
∴k＝h2+h+1，
∴mh2+nh+1＝h2+h+1，
∴
，
又∵﹣1＜h＜1，
∴m＜﹣2或m＞0．
