题目内容
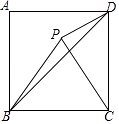
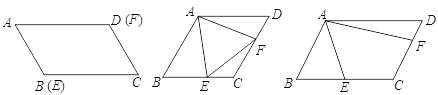
【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.
【答案】
(1)
证明:连接FD交EC于P,
由折叠矩形ABCD可得,EF=ED,CF=CD,∠DEC=∠FEC,∠EFG=∠EFC=∠EDC=90°,
∵点E为AD的中点,
∴AE=ED=EF,
∴∠EAF=∠EFA,
∵∠DEF=∠EAF+∠EFA=∠DEC+∠FEC,
∴∠EAF=∠DEC,
∴AF∥EC;
(2)
∵EF=ED,CF=CD,
∴E,C两点都在线段DF的中垂线上,即EC⊥DF,
∴∠DPE=90°,
∵AF∥EC,
∴∠AFD=∠DPE=∠EDC=90°,
∵∠EAF=∠DEC,∠AFD=∠EDC,
∴△AFD∽△EDC,
∴ ![]() ,即AFEC=DEAD,
,即AFEC=DEAD,
∴AFEC=2EF2;
(3)
∵∠GAF+∠EAF=∠GFA+∠EFA=90°,∠EAF=∠EFA,
∴∠GAF=∠GFA,
∴AG=FG,
在Rt△BGC中,BC=6,BG=8,
CG= ![]() =10,
=10,
∵AB=CD=CF,
∴8+AG=10﹣FG,
∴AG=FG=1,
∴CF=CD=9,
∵AD=BC=6,
∴EF= ![]() AD=3,
AD=3,
∴在Rt△DEC中,EC= ![]() =3
=3 ![]() ,
,
∵AFEC=2EF2,
∴3 ![]() ×AF=2×32,
×AF=2×32,
解得,AF= ![]() .
.
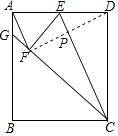
【解析】(1)连接FD交EC于P,根据折叠的性质得到EF=ED,CF=CD,∠DEC=∠FEC,∠EFG=∠EFC=∠EDC=90°,根据直角三角形的性质得到AE=ED=EF,求出∠EAF=∠DEC,根据平行线的判定定理证明;(2)证明△AFD∽△EDC,根据相似三角形的性质定理计算即可;(3)根据勾股定理求出CG,根据矩形的性质求出AB,根据(2)的结论计算即可.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案