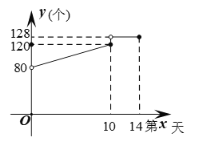
题目内容
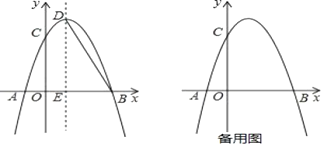
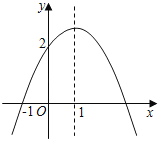
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),与y轴交于(0,2),抛物线的对称轴为直线x=1,则下列结论中:①a+c=b;②方程ax2+bx+c=0的解为﹣1和3;③2a+b=0;④c﹣a>2,其中正确的结论有( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴x=1计算2a+b与偶的关系,进而对所得结论进行判断.
解:①∵抛物线y=ax2+bx+c经过点(﹣1,0),
∴a﹣b+c=0,
∴a+c=b,故本选项正确;
②由对称轴为x=1,一个交点为(﹣1,0),
∴另一个交点为(3,0),
∴方程ax2+bx+c=0的解为﹣1和3,故本选项正确;
③由对称轴为x=1,
∴﹣![]() =1,
=1,
∴b=﹣2a,则2a+b=0,故本选项正确;
④∵抛物线y=ax2+bx+c与y轴交于(0,2),
∴c=2,
∵a<0,
∴c﹣a>2,故本选项正确;
故选:D.

【题目】为了迎接体育理化加试,九(2)班同学到某体育用品商店采购训练用球,已知购买3个A品牌足球和2个B品牌足球需付210元;购买2个A品牌足球和1个B品牌足球需付费130元.(优惠措施见海报)巨惠来袭(解释权归本店所有)
A品牌 | B品牌 |
|
|
单品数量低于40个不优惠,高于40个 享8折优惠 | 单品数量低于40个不优惠,高于40个 享9折优惠 |
(1)求A,B两品牌足球的单价各为多少元?
(2)为享受优惠,同学们决定购买一次性购买足球60个,若要求A品牌足球的数量不低于B品牌足球数量的3倍,请你设计一种付费最少的方案,并说明理由.
【题目】为提升学生的数学素养,某学校开展了“数学素养”竞赛活动.九年级![]() 名学生参加了竞赛,结果所有学生成绩都不低于
名学生参加了竞赛,结果所有学生成绩都不低于![]() 分(满分
分(满分![]() 分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中所给信息,解答下列问题:
分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表,根据表中所给信息,解答下列问题:
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
![]() 表中
表中![]() ___ _ _ ,
___ _ _ ,![]() _;
_;
![]() 这组数据的中位数落在_____ _范围内;
这组数据的中位数落在_____ _范围内;
![]() 若成绩不小于
若成绩不小于![]() 分为优秀,请估计九年级大约有多少名学生获得优秀成绩?
分为优秀,请估计九年级大约有多少名学生获得优秀成绩?
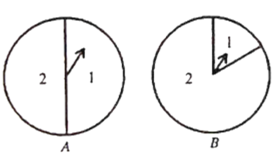
![]() 竞赛中有这样一道题目: 如图,有两个转盘
竞赛中有这样一道题目: 如图,有两个转盘![]() 在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘
在每个转盘各自的两个扇形区域中分别标有数字1,2,分别转动转盘![]() 当转盘停止转动时,若事件“指针都落在标有数字
当转盘停止转动时,若事件“指针都落在标有数字![]() 的扇形区域内”概率是
的扇形区域内”概率是![]() ,则转盘
,则转盘![]() 中标有数字
中标有数字![]() 的扇形的圆心角的度数是 .
的扇形的圆心角的度数是 .