Question

【题目】已知：在△ABC中，∠ABC=90°，AB=BC，点D为线段BC上一动点（点D不与点B、C重合），点B关于直线AD的对称点为E，作射线DE，过点C作BC的垂线，交射线DE于点F，连接AE．

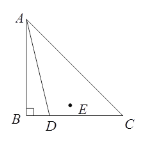
（1）依题意补全图形；

（2）AE与DF的位置关系是 ；

（3）连接AF，小昊通过观察、实验，提出猜想：发现点D 在运动变化的过程中，∠DAF的度数始终保持不变，小昊把这个猜想与同学们进行了交流，经过测量，小昊猜想∠DAF= °，通过讨论，形成了证明该猜想的两种想法：

想法1：过点A作AG⊥CF于点G，构造正方形ABCG，然后可证△AFG≌△AFE……

想法2：过点B作BG∥AF，交直线FC于点G，构造□ABGF，然后可证△AFE≌△BGC……

请你参考上面的想法，帮助小昊完成证明（一种方法即可）．

Answer 1

【答案】（1）详见解析；（2）互相垂直；（3）45°，证明详见解析

【解析】

（1）根据题意正确画图；
（2）证明△ABD≌△AED（SSS），可得∠AED=∠B=90°，从而得结论；
（3）想法1：如图2，过点A做AG⊥CF于点G，先证明四边形ABCG是正方形，得AG=AB，∠BAG=90°，再证明Rt△AFG≌Rt△AFE（HL），得∠GAF=∠EAF，根据∠BAG=90°及角的和可得结论；
想法2：如图3，过点B作BG∥AF，交直线FC于点G，证明四边形ABGF是平行四边形，得AF=BG，∠BGC=∠BAF，再证明Rt△AEF≌Rt△BCG （HL），同理根据∠BCG=90°及等量代换，角的和可得结论．

（1）补全图形如下：

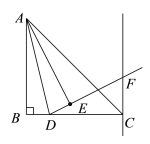
（2）AE与DF的位置关系是：AE⊥DF，
理由是：∵点B关于直线AD的对称点为E，
∴AB=AE，BD=DE，
∵AD=AD，
∴△ABD≌△AED（SSS），
∴∠AED=∠B=90°，
∴AE⊥DF；
故答案为：AE⊥DF；
（3）猜想∠DAF=45°；
想法1：
证明如下：如图2，过点A做AG⊥CF于点G，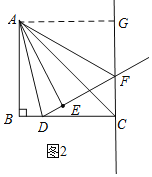

依题意可知：∠B=∠BCG=∠CGA=90°，
∵AB=BC，
∴四边形ABCG是正方形，
∴AG=AB，∠BAG=90°，
∵点B关于直线AD的对称点为E，
∴AB=AE，∠B=∠AED=∠AEF=90°，∠BAD=∠EAD，
∴AG=AE，
∵AF=AF，
∴Rt△AFG≌Rt△AFE（HL），
∴∠GAF=∠EAF，
∵∠BAG=90°，
∴∠BAD+∠EAD+∠EAF+∠GAF=90°，
∴∠EAD+∠EAF=45°．
即∠DAF=45°．
想法2：
证明如下：如图3，过点B作BG∥AF，交直线FC于点G，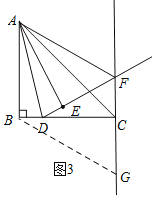

依题意可知：∠ABC=∠BCF=90°，
∴AB∥FG，
∵AF∥BG，
∴四边形ABGF是平行四边形，
∴AF=BG，∠BGC=∠BAF，
∵点B关于直线AD的对称点为E，
∴AB=AE，∠ABC=∠AED=90°，∠BAD=∠EAD，
∵AB=BC，
∴AE=BC，
∴Rt△AEF≌Rt△BCG （HL），
∴∠EAF=∠CBG，
∵∠BCG=90°，
∴∠BGC+∠CBG=90°，
∴∠BAF+∠EAF=90°，
∴∠BAD+∠EAD+∠EAF+∠EAF=90°，
∵∠BAD=∠EAD，
∴∠EAD+∠EAF=45°，
即∠DAF=45°．
故答案为：45．