��Ŀ����
����Ŀ��Ϊ����ѧ������ѧ������ijѧУ��չ�ˡ���ѧ�����������.���꼶![]() ��ѧ���μ��˾������������ѧ���ɼ���������
��ѧ���μ��˾������������ѧ���ɼ���������![]() ��(����
��(����![]() ��)��Ϊ���˽�ɼ��ֲ������ѧУ�����ȡ�˲���ѧ���ijɼ�����ͳ�ƣ��õ����²�������ͳ�Ʊ������ݱ���������Ϣ������������⣺
��)��Ϊ���˽�ɼ��ֲ������ѧУ�����ȡ�˲���ѧ���ijɼ�����ͳ�ƣ��õ����²�������ͳ�Ʊ������ݱ���������Ϣ������������⣺
�ɼ� | Ƶ�� | Ƶ�� |
|
|
|
|
|
|
|
|
|
|
|
|
![]() ����
����![]() ___ _ _ ��
___ _ _ ��![]() _��
_��
![]() �������ݵ���λ������_____ _��Χ�ڣ�
�������ݵ���λ������_____ _��Χ�ڣ�
![]() ���ɼ���С��
���ɼ���С��![]() ��Ϊ���㣬����ƾ��꼶��Լ�ж�����ѧ���������ɼ���
��Ϊ���㣬����ƾ��꼶��Լ�ж�����ѧ���������ɼ���
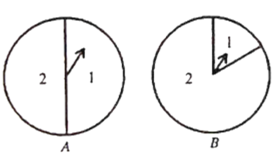
![]() ������������һ����Ŀ�� ��ͼ��������ת��
������������һ����Ŀ�� ��ͼ��������ת��![]() ��ÿ��ת�̸��Ե��������������зֱ��������1��2���ֱ�ת��ת��
��ÿ��ת�̸��Ե��������������зֱ��������1��2���ֱ�ת��ת��![]() ��ת��ֹͣת��ʱ�����¼���ָ�붼���ڱ�������
��ת��ֹͣת��ʱ�����¼���ָ�붼���ڱ�������![]() �����������ڡ�������
�����������ڡ�������![]() ����ת��
����ת��![]() �б�������
�б�������![]() �����ε�Բ�ĽǵĶ����� ��
�����ε�Բ�ĽǵĶ����� ��
���𰸡�![]()
![]() ��
��![]() ��
�� ![]() �����
��λ����![]() �ڣ�
�ڣ� ![]() ����
����![]()
��������
��1���ȸ���![]() �����������Ϊ50��ѧ�����ĸ�����������;���50���������
�����������Ϊ50��ѧ�����ĸ�����������;���50���������![]() ��ֵ��������֪
��ֵ��������֪![]() ��Ƶ�����������������
��Ƶ�����������������![]() ��
��
��2��������λ���ĸ��������𰸣�
��3�����������гɼ���С��![]() ��Ϊ�����Ƶ�ʼ��ɹ��������гɼ���С��
��Ϊ�����Ƶ�ʼ��ɹ��������гɼ���С��![]() �ֵ�ѧ��������
�ֵ�ѧ��������
��4���ȸ����������ת��B��ָ�����ڱ�������1�����������ڵĸ��ʣ��ٸ���Բ�ܽǵ���![]() ���㼴�ɣ�
���㼴�ɣ�
�⣺��1������ѧ��������![]() ��������
��������
![]() ��Ƶ����
��Ƶ����![]() ����
����![]() ��
��
![]() ��Ƶ�ʣ�
��Ƶ�ʣ�![]() ����
����![]() ��
��
�ʴ�Ϊ��20��0.2��
��2����50��ѧ������λ�����ڡ�![]() ����Χ�ڣ�
����Χ�ڣ�
��3������ѧ���У��ɼ���С��![]() �ֵ�Ƶ�ʣ�
�ֵ�Ƶ�ʣ�![]() ��
��
���Ը��������������壬���꼶�������ɼ���ѧ��������![]() ��������
��������
�����꼶��Լ��360��ѧ���������ɼ���
��4����ת��B��ָ�����ڱ�������1�����������ڵĸ���Ϊ![]() ��
��
��������ã�![]() ��
��
���![]() ��
��
����ת��B��ָ�����ڱ�������1�����ε�Բ�ĽǵĶ���Ϊ��![]() ��
��
�ʴ�Ϊ��![]() ��
��