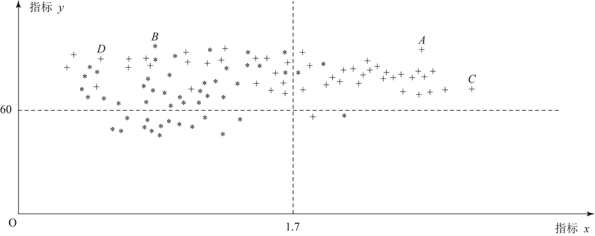
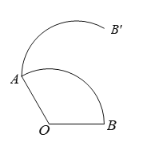
题目内容
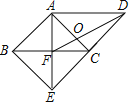
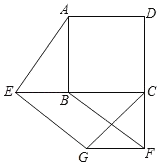
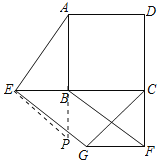
【题目】如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.
(1)求∠AEG的度数;
(2)求证:四边形BEGF是平行四边形.
【答案】(1)90°;(2)证明见解析.
【解析】
(1)由SAS证明△ABE≌△BCF得出AE=BF,∠BAE=∠CBF,由平行线的性质得出∠CBF=∠CEG,证出AE⊥EG,即可得出结论;
(2)延长AB至点P,使BP=BE,连接EP,则AP=CE,∠EBP=90°,证明△APE≌△ECG得出AE=EG,证出EG=BF,即可得出结论.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,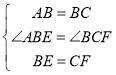
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴∠AEG的度数为90°;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,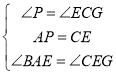
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.

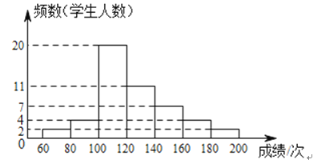
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
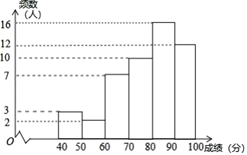
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.