题目内容
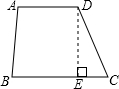
梯形ABCD中，AD∥CB，AB⊥BC，∠C=60°，BC=CD=4cm，则AD=______cm，AB=______cm，S梯形ABCD=______cm2．
作DE⊥BC，
∵AB⊥BC
∴四边形ABDE为矩形
∵∠C=60°，BC=CD=4cm
∴AB=DE=sin60°•DC=2
，EC=
DC=2
∴AD=BE=BC-EC=2
∴梯形的面积是：
×（2+4）×2
=6
∵AB⊥BC
∴四边形ABDE为矩形
∵∠C=60°，BC=CD=4cm
∴AB=DE=sin60°•DC=2
| 3 |
| 1 |
| 2 |
∴AD=BE=BC-EC=2
∴梯形的面积是：
| 1 |
| 2 |
| 3 |
| 3 |
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
