题目内容
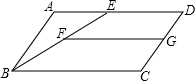
如图所示，已知等腰梯形ABCD中，AD∥BC，下底BC与上底AD的差恰好等于腰长AB，则∠BAD=（ ）
| A．120° | B．135° | C．150° | D．60° |
过点A作AE∥CD，交BC于点E，
∵等腰梯形ABCD中，AD∥BC，AB=CD，
∴四边形AECD是平行四边形，
∴EC=AD，AE=CD，
∴AE=AB，
∵下底BC与上底AD的差恰好等于腰长AB，
∴BE=BC-EC=BC-AD=AB，
∴AB=AE=BE，
即△ABE是等边三角形，
∴∠B=60°，
∴∠BAC=120°．
故选A．
∵等腰梯形ABCD中，AD∥BC，AB=CD，
∴四边形AECD是平行四边形，
∴EC=AD，AE=CD，
∴AE=AB，
∵下底BC与上底AD的差恰好等于腰长AB，
∴BE=BC-EC=BC-AD=AB，
∴AB=AE=BE，
即△ABE是等边三角形，
∴∠B=60°，
∴∠BAC=120°．
故选A．
练习册系列答案
相关题目
，点P与AD在直线EF的两侧，∠EPF=90°，PE=PF，射线EP、FP与边BC分别相交于点M、N，设AE=x，MN=y．
出相应的t的值和P、Q的坐标；如不可能，请说明理由．
