题目内容
如图，直角梯形ABCD中，AD∥BC，∠A=90，BC=CD，BE⊥CD，垂足为E
（1）求证：AB=BE；
（2）若AD=1，AB=2，求BC的长．
（1）求证：AB=BE；
（2）若AD=1，AB=2，求BC的长．
证明（1）过点D作DH⊥BC于H，
在△DHC和BEC中，
∵
，
∴△DHC≌△BEC，
∴DH=BE，
∵∠A=∠ABC=∠DHB=90
∴四边形ABHD是矩形，
∴AB=DH，
∴AB=BE；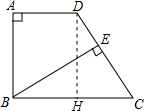
（2）设CD=BC=x，则HC=BC-BH=x-1，
在Rt△DHC中，
DH2+HC2=DC2，
即（x-1）2+22=x2，
解得：x=2.5，
则BC=2.5．
在△DHC和BEC中，
∵
|
∴△DHC≌△BEC，
∴DH=BE，
∵∠A=∠ABC=∠DHB=90
∴四边形ABHD是矩形，
∴AB=DH，
∴AB=BE；
（2）设CD=BC=x，则HC=BC-BH=x-1，
在Rt△DHC中，
DH2+HC2=DC2，
即（x-1）2+22=x2，
解得：x=2.5，
则BC=2.5．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
