题目内容
如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M从A点开始,沿AD边向D运动,速度为1厘米/秒,点N从点C开始沿CB边向点B运动,速度为2厘米/秒,设四边形MNCD的面积为S.
(1)写出面积S与时间t之间的函数关系式;
(2)当t为何值时,四边形MNCD是平行四边形?
(3)当t为何值时,四边形MNCD是等腰梯形?

(1)写出面积S与时间t之间的函数关系式;
(2)当t为何值时,四边形MNCD是平行四边形?
(3)当t为何值时,四边形MNCD是等腰梯形?

(1)根据题意得:AM=tcm,CN=2tcm,则MD=AD-AM=15-t(cm),
∴S=
(MD+CN)•AB=
×(15-t+2t)×14=7t+105(cm2);
∴面积S与时间t之间的函数关系式为:S=7t+105;
(2)∵点M的速度为1cm/s,点N的速度为2cm/s,
∴MD=AD-AM=15-t,CN=2t,
四边形MNCD是平行四边形时,MD=CN,
∴15-t=2t,
解得t=5;
∴当t=5时,四边形MNCD是平行四边形;
(3)如图,过点D作DE⊥BC于E,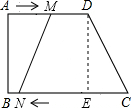
∵AD∥BC,∠B=90°,
∴四边形ABED是矩形,
∴BE=AD=15cm,
∴CE=BC-BE=21-15=6cm,
四边形MNCD是等腰梯形时,CN=2CE+MD,
∴2t=2×6+15-t,
解得t=9.
∴当t=9时,四边形MNCD是等腰梯形.
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴面积S与时间t之间的函数关系式为:S=7t+105;
(2)∵点M的速度为1cm/s,点N的速度为2cm/s,
∴MD=AD-AM=15-t,CN=2t,
四边形MNCD是平行四边形时,MD=CN,
∴15-t=2t,
解得t=5;
∴当t=5时,四边形MNCD是平行四边形;
(3)如图,过点D作DE⊥BC于E,

∵AD∥BC,∠B=90°,
∴四边形ABED是矩形,
∴BE=AD=15cm,
∴CE=BC-BE=21-15=6cm,
四边形MNCD是等腰梯形时,CN=2CE+MD,
∴2t=2×6+15-t,
解得t=9.
∴当t=9时,四边形MNCD是等腰梯形.

练习册系列答案
相关题目


 出相应的t的值和P、Q的坐标;如不可能,请说明理由.
出相应的t的值和P、Q的坐标;如不可能,请说明理由.