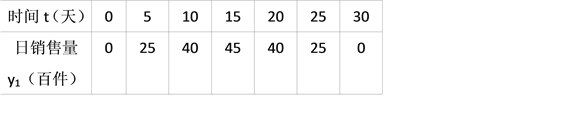题目内容
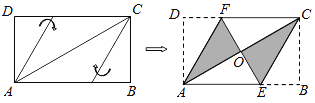
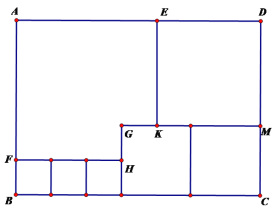
【题目】如图所示，用三种大小不同的六个正方形和一个缺角的长方形拼成大长方形ABCD，其中GH=1，GK=1，设BF=a.
(1)用含a的代数式表示CM=_____cm，DM=_______cm.
(2)用含a的代数式表示大长方形ABCD的周长.
【答案】(1)a+1；2a+1；(2)周长=16a+8.
【解析】
（1）根据图中可知CM=BF+GH，DM=KM=CM+(CM-GK)即可得出答案；
（2）结合（1）分别用含a的代数式表示出BC和CD即可求出答案.
解：（1）由图中可知CM=BF+GH，因为BF=a，GH=1，所以CM=a+1，
由图中可知DM=KM=CM+(CM-GK)，因为CM=a+1，GK=1，所以CM-GK=a，所以DM=a+1+a=2a+1；
（2）由（1）可知DM=2a+1，CM=a+1，CD=DM+CM，
所以CD=3a+2，
由图中可知BC=3BF+2CM，所以BC=3a+2(a+1)=5a+2
所以长方形ABCD的周长为2（BC+CD）=2（3a+2+5a+2）=16a+8，
故答案为a+1；2a+1；周长=16a+8.
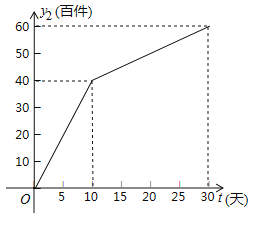
【题目】如图，动点
从
出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点第
次碰到矩形的边时，点的坐标为（ ）
A. (0,3) B. (5,0) C. (1,4) D. (8,3)
【题目】利民商场经营某种品牌的T恤，购进时的单价是300元，根据市场调查：在一段时间内，销售单价是400元时，销售量是60件，销售单价每涨10元，销售量就减少1件．设这种T恤的销售单价为x元（x＞400）时，销售量为y件、销售利润为W元．
（1）请分别用含x的代数式表示y和W（把结果填入下表）：
销售单价（元） | x |
销售量y（件） | |
销售利润W（元） |
（2）该商场计划实现销售利润10000元，并尽可能增加销售量，那么x的值应当是多少？
