题目内容
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为 ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
【答案】(![]() ,0)
,0)
【解析】试题解析:过点B作BD⊥x轴于点D,
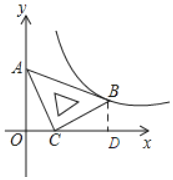
∵∠ACO+∠BCD=90°,
∠OAC+∠ACO=90°,
∴∠OAC=∠BCD,
在△ACO与△BCD中,
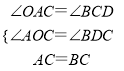 ,
,
∴△ACO≌△BCD(AAS)
∴OC=BD,OA=CD,
∵A(0,2),C(1,0)
∴OD=3,BD=1,
∴B(3,1),
∴设反比例函数的解析式为y=![]() ,
,
将B(3,1)代入y=![]() ,
,
∴k=3,
∴y=![]() ,
,
∴把y=2代入y=![]() ,
,
∴x=![]() ,
,
当顶点A恰好落在该双曲线上时,
此时点A移动了![]() 个单位长度,
个单位长度,
∴C也移动了![]() 个单位长度,
个单位长度,
此时点C的对应点C′的坐标为(![]() ,0)
,0)
故答案为:(![]() ,0).
,0).

练习册系列答案
相关题目