题目内容
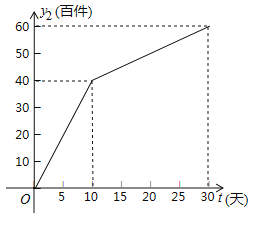
【题目】（2017湖北省荆门市）我市雷雷服饰有限公司生产了一款夏季服装，通过实体商店和网上商店两种途径进行销售，销售一段时间后，该公司对这种商品的销售情况，进行了为期30天的跟踪调查，其中实体商店的日销售量y1（百件）与时间t（t为整数，单位：天）的部分对应值如下表所示，网上商店的日销售量y2（百件）与时间t（t为整数，单位：天）的部分对应值如图所示．
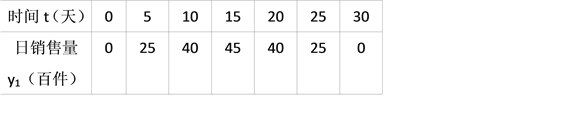
（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数能反映y1与t的变化规律，并求出y1与t的函数关系式及自变量t的取值范围；
（2）求y2与t的函数关系式，并写出自变量t的取值范围；
（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为y（百件），求y与t的函数关系式；当t为何值时，日销售总量y达到最大，并求出此时的最大值．
【答案】（1）
（0≤t≤30，且为整数）；（2）
；（3）
，当t=17或18时，y最大=91.2百件．
【解析】试题分析：（1）根据观察可设y1=at2+bt+c，将（0，0），（5，25），（10，40）代入即可得到结论；
（2）当0≤t≤10时，设y2=kt，求得y2与t的函数关系式为：y2=4t，当10≤t≤30时，设y2=mt+n，将（10，40），（30，60）代入得到y2与t的函数关系式为：y2=k+30，（3）依题意得y=y1+y2，当0≤t≤10时，得到y最大=80；当10＜t≤30时，得到y最大=91.2，于是得到结论．
试题解析：解（1）根据观察可设
，将（0，0），（5，25），（10，40）代入得： 
，解得： 
，∴y1与t的函数关系式为： 
（0≤t≤30，且为整数）；
（2）当0≤t≤10时，设y2=kt，∵（10，40）在其图象上，∴10k=40，∴k=4，∴y2与t的函数关系式为：y2=4t，当10≤t≤30时，设y2=mt+n，将（10，40），（30，60）代入得： 
，解得： 
，∴y2与t的函数关系式为：y2=t+30，综上所述， 
；
（3）依题意得y=y1+y2，当0≤t≤10时，y=
=
=
（t﹣25）2+125，∴t=10时，y最大=80；
当10＜t≤30时，y=
t2+6t+t+30=
=
，∵t为整数，∴t=17或18时，y最大=91.2，∵91.2＞80，∴当t=17或18时，y最大=91.2（百件）．
综上所述： 
，当t=17或18时，y最大=91.2百件．
科学实验活动册系列答案
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神，某校特制定了一系列帮扶A、B两贫困村的计划，现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如表：
车型 | 目的地 | |
A村（元/辆） | B村（元/辆） | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
（1）求这15辆车中大小货车各多少辆？
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．
