题目内容
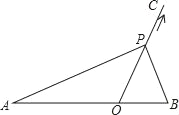
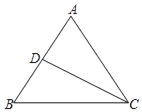
【题目】如图，在△ABC中，AB=AC，BC=8，tanB=
，点D是AB的中点，如果把△BCD沿直线CD翻折，使得点B落在同一平面内的B′处，联结A B′，那么A B′的长为_____．
【答案】
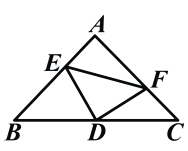
【解析】分析：如图，作AE⊥BC于E，DK⊥BC于K，连接BB′交CD于H．只要证明∠AB′B=90°，求出AB、BB′，理由勾股定理即可解决问题；
详解：如图，作AE⊥BC于E，DK⊥BC于K，连接BB′交CD于H．
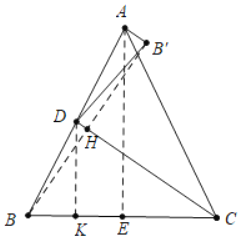
∵AB=AC，AE⊥BC，
∴BE=EC=4，
在Rt△ABE中，∵tanB=
，
∴AE=6，AB=
=2
，
∵DK∥AE，BD=AD，
∴BK=EK=2，
∴DK=
AE=3，
在Rt△CDK中，CD=
，
∵B、B′关于CD对称，
∴BB′⊥CD，BH=HB′
∵S△BDC=BCDK=CDBH，
∴BH=
，
∴BB′=
，
∵BD=AD=DB′，
∴∠AB′B=90°，
∴AB′=
，
故答案为:
练习册系列答案
相关题目
【题目】王大伯承包了25亩土地，今年春季改种茄子和西红柿两种大棚蔬菜，其中种茄子每亩可获利2400元，种西红柿每亩可获利2600元，王大伯一共获纯利多少元．
（1）若设种茄子x亩，用含有x的式子填下表:
亩数 | 每亩可获利 | 总获利 | |
茄子 | |||
西红柿 |
（2）王大伯种两种蔬菜一共获纯利多少元．（用含x的代数式表示）
