题目内容
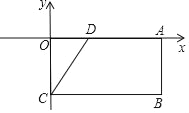
【题目】如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x轴与y轴上,D为OA上一点,且CD=AD.
(1)求过点B、C、D的抛物线的解析式;
(2)求出(1)中抛物线与x轴的另一个交点E坐标.
【答案】(1)过点B、C、D的抛物线的解析式是y=﹣![]() x2+
x2+![]() x﹣4;(2)点E坐标是(5,0).
x﹣4;(2)点E坐标是(5,0).
【解析】试题分析:(1)根据勾股定理求出OD,得出C、B、D的坐标,代入函数解析式,即可求出答案;
(2)把y=0代入函数解析式,求出x即可.
试题解析:(1)在Rt△DOC中,由勾股定理得:OD2+OC2=CD2,
即OD2+42=(8-OD)2,
解得:OD=3,
设抛物线的解析式为y=ax2+bx+c(a≠0),
由题意得:B(8,-4),C(0,-4),D(3,0),
代入解析式得: 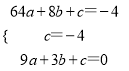 ,
,
解得:a=-![]() ,b=
,b=![]() ,c=-4,
,c=-4,
即过点B、C、D的抛物线的解析式是y=-![]() x2+
x2+![]() x-4;
x-4;
(2)把y=0代入y=--![]() x2+
x2+![]() x-4得:--
x-4得:--![]() x2+
x2+![]() x-4=0,
x-4=0,
解得:x=3和5,
即(1)中抛物线与x轴的另一个交点E坐标是(5,0).

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目