题目内容
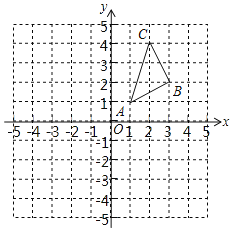
【题目】已知:图①、图②是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点![]() 、点
、点![]() 和点
和点![]() 均在小正方形的顶点上.请在图①、图②中各画一个四边形,满足以下要求:
均在小正方形的顶点上.请在图①、图②中各画一个四边形,满足以下要求:

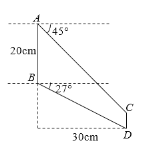
(1)在图①中以![]() 和
和![]() 为边画四边形
为边画四边形![]() ,点
,点![]() 在小正方形的顶点上,且此四边形四个内角中有一个角为45°;
在小正方形的顶点上,且此四边形四个内角中有一个角为45°;
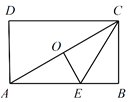
(2)在图②中以![]() 和
和![]() 为边画四边形
为边画四边形![]() ,点
,点![]() 在小正方形的顶点上,且此四边形对角互补,并且四个内角中有一个角为钝角;
在小正方形的顶点上,且此四边形对角互补,并且四个内角中有一个角为钝角;
(3)请直接写出图②中![]() 的正切值.
的正切值.
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)利用数形结合的思想解决问题即可.
(2)利用数形结合的思想思考问题即可解决问题.
(3)作BH⊥CE于H,求出BH,CH即可解决问题.
(1)如图,四边形ABCD即为所求.
(2)如图,四边形ABCE即为所求.

(3)作BH⊥EC于H.
∵S△BCE=![]() ECBH=
ECBH=![]() ×4×4,BC=CE=
×4×4,BC=CE=![]() ,
,
∴BH=![]() ,
,
∴CH=![]() =
= ,
,
∴tan∠BCE=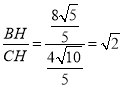 .
.

【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | |
甲 | 9 | 8 | 8 | 7 |
乙 | 10 | 6 | 7 | 9 |
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩;
(2)分别计算甲、乙两人四次测试成绩的方差;根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
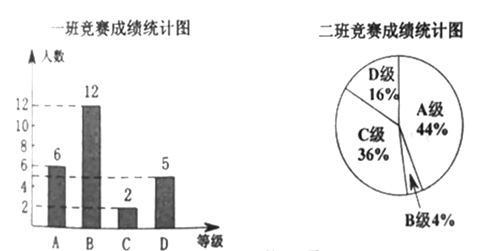
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)