题目内容
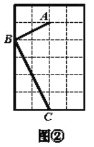
【题目】如图,正方形网格中,每一个小正方形的边长都是1个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,1),B(3,2),C(2,4).
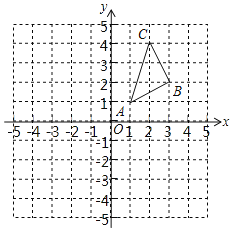
(1)画出△ABC关于x轴对称的△A1B1C1,直接写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求BC边所扫过的面积.(结果保留π)
【答案】(1)如图,△A1B1C1即为所求,见解析;点A1的坐标为:(1,﹣1);(2)△A2B2C2即为所求,见解析;(3)BC边所扫过的面积是![]() .
.
【解析】
(1)根据关于x轴对称的点的横坐标不变,纵坐标互为相反数,即可作出△ABC关于x轴对称的△A1B1C1,进而得出点A1的坐标;
(2)分别确定△ABC三个顶点绕点O逆时针旋转90°后的点,再连接即可得到△A2B2C2;
(3)先利用勾股定理解直角三角形,求得OB2和OC2,BC边所扫过的面积为S扇形OCC2-S扇形OBB2,利用扇形面积计算公式即可求解.
(1)如图,分别画出△ABC三个顶点A、B、C关于x轴对称的点A1、B1、C1,再连接点A1、B1、C1,△A1B1C1即为所求;
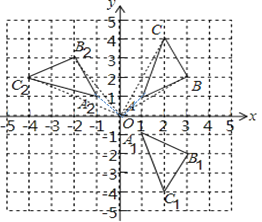
∵A(1,1),点A和A1关于x轴对称
∴点A1的坐标为:(1,﹣1)
故答案为:作图见解析,点A1的坐标为(1,﹣1)
(2)连接OA、OB、OC,将OA、OB、OC绕点O逆时针旋转90°后得到OA2、OB2、OC2,连接点A2、B2、C2,△A2B2C2即为所求;
(3)∵OB2=32+22=13,
OC2=42+22=20,
∴BC边所扫过的面积为:S扇形OCC2-S扇形OBB2=![]()
故答案为:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目