题目内容
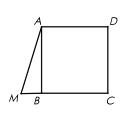
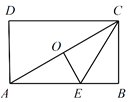
【题目】如图,点![]() 是矩形
是矩形![]() 两条对角线的交点,E是边
两条对角线的交点,E是边![]() 上的点,沿
上的点,沿![]() 折叠后,点
折叠后,点![]() 恰好与点
恰好与点![]() 重合.若
重合.若![]() ,则折痕
,则折痕![]() 的长为 ( )
的长为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
【答案】A
【解析】
由矩形的性质可得OA=OC,根据折叠的性质可得OC=BC,∠COE=∠B=90°,即可得出BC=![]() AC,OE是AC的垂直平分线,可得∠BAC=30°,根据垂直平分线的性质可得CE=AE,根据等腰三角形的性质可得∠OCE=∠BAC=30°,在Rt△OCE中利用含30°角的直角三角形的性质即可求出CE的长.
AC,OE是AC的垂直平分线,可得∠BAC=30°,根据垂直平分线的性质可得CE=AE,根据等腰三角形的性质可得∠OCE=∠BAC=30°,在Rt△OCE中利用含30°角的直角三角形的性质即可求出CE的长.
∵点O是矩形ABCD两条对角线的交点,
∴OA=OC,
∵沿CE折叠后,点B恰好与点O重合.BC=3,
∴OC=BC=3,∠COE=∠B=90°,
∴AC=2BC=6,OE是AC的垂直平分线,
∴AE=CE,
∵∠B=90°,BC=![]() AC,
AC,
∴∠BAC=30°,
∴∠OCE=∠BAC=30°,
∴OC=![]() CE,
CE,
∴CE=2![]() .
.
故选A.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】长江中下游地区特大旱情发生后,全国人民抗旱救灾,众志成城.市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
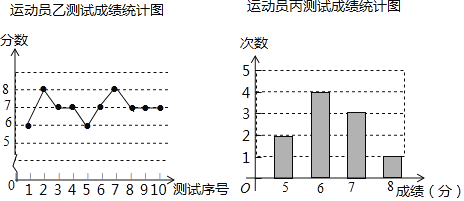
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)