Question

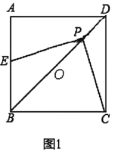
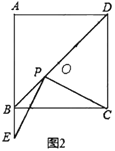
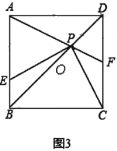
【题目】如图，四边形ABCD中，AD∥BC，∠D＝90°，AD＝4，BC＝3．分别以点A，C为圆心，大于AC长为半径作弧，两弧交于点E，射线BE交AD于点F，交AC于点O．若点O恰好是AC的中点，则CD的长为__．

Answer 1

【答案】2

【解析】

根据作图过程可得，BF是AC的垂直平分线，然后证明△AOF≌△COB，得AF＝BC＝FC＝3，再根据勾股定理即可求出CD的长．

解：由作图过程可知：

BF是AC的垂直平分线，

∴AF＝CF，AO＝CO，

∵AD∥BC，

∴∠AFO＝∠CBO，

又∵∠AOF＝∠COB，

∴△AOF≌△COB（AAS），

∴AF＝BC＝3，

∴FC＝AF＝3，

∴FD＝AD﹣AF＝4﹣3＝1，

在Rt△FCD中，根据勾股定理，得

CD＝．

∴CD的长为．

故答案为：．