题目内容
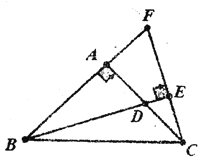
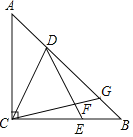
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)EF=![]()
【解析】(1)由翻折知△ABC≌△ABD,得∠ADB=∠C=90°,据此即可得;
(2)由AB=AD知AB2=ADAE,即![]() ,据此可得△ABD∽△AEB,即可得出∠ABE=∠ADB=90°,从而得证;
,据此可得△ABD∽△AEB,即可得出∠ABE=∠ADB=90°,从而得证;
(3)由![]() 知DE=1、BE=
知DE=1、BE=![]() ,证△FBE∽△FAB得
,证△FBE∽△FAB得![]() ,据此知FB=2FE,在Rt△ACF中根据AF2=AC2+CF2可得关于EF的一元二次方程,解之可得.
,据此知FB=2FE,在Rt△ACF中根据AF2=AC2+CF2可得关于EF的一元二次方程,解之可得.
(1)∵AB为⊙O的直径,
∴∠C=90°,
∵将△ABC沿AB翻折后得到△ABD,
∴△ABC≌△ABD,
∴∠ADB=∠C=90°,
∴点D在以AB为直径的⊙O上;
(2)∵△ABC≌△ABD,
∴AC=AD,
∵AB2=ACAE,
∴AB2=ADAE,即![]() ,
,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴∠ABE=∠ADB=90°,
∵AB为⊙O的直径,
∴BE是⊙O的切线;
(3)∵AD=AC=4、BD=BC=2,∠ADB=90°,
∴AB=![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:DE=1,
∴BE=![]() ,
,
∵四边形ACBD内接于⊙O,
∴∠FBD=∠FAC,即∠FBE+∠DBE=∠BAE+∠BAC,
又∵∠DBE+∠ABD=∠BAE+∠ABD=90°,
∴∠DBE=∠BAE,
∴∠FBE=∠BAC,
又∠BAC=∠BAD,
∴∠FBE=∠BAD,
∴△FBE∽△FAB,
∴![]() ,即
,即![]() ,
,
∴FB=2FE,
在Rt△ACF中,∵AF2=AC2+CF2,
∴(5+EF)2=42+(2+2EF)2,
整理,得:3EF2-2EF-5=0,
解得:EF=-1(舍)或EF=![]() ,
,
∴EF=![]() .
.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案