题目内容
若⊙O半径为3，OP＝1，⊙P与⊙O相切，则⊙P的半径为 ____．
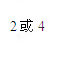
先根据⊙O半径为3，OP=1，⊙P与⊙O相切可知⊙O与⊙P内切，再设⊙P的半径为r，利用两圆内切的特点列出关于r的方程，求出r的值即可．
解答：解：∵⊙O半径为3，OP=1，⊙P与⊙O相切，
∴⊙O与⊙P内切，
设⊙P的半径为r，则3-r=1或r-3=1，
解得r=2或r=4．
故答案为：2或4．
解答：解：∵⊙O半径为3，OP=1，⊙P与⊙O相切，
∴⊙O与⊙P内切，
设⊙P的半径为r，则3-r=1或r-3=1，
解得r=2或r=4．
故答案为：2或4．
练习册系列答案
相关题目
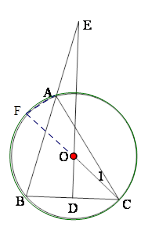
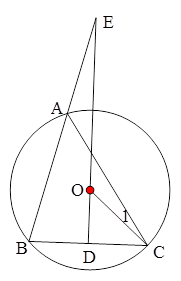
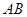是⊙O的直径,
切⊙O于点
,且
为等腰三角形,若存在,有几个符合条件的点
,并分别求出点
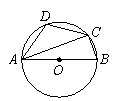
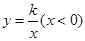的图像过点P，则
＝ .
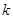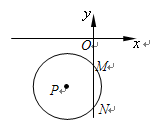
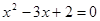的两个根，则它们的圆心距
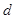的取值范围是 ．