题目内容
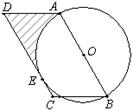
如图，AB是⊙O的直径，C、D是⊙O上的两点，若∠BAC=20°，AD=DC，则∠DAC的度数是（ ）
| A．30° | B．35° | C．45° | D．70° |
B
解：连接OC，OD，如图所示：
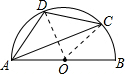
∵∠BAC与∠BOC所对的弧都为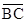
，∠BAC=20°，
∴∠BOC=2∠BAC=40°，
∴∠AOC=140°，
又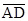
=
，
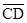∴∠COD=∠AOD=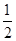
∠AOC=70°，
∵∠DAC与∠DOC所对的弧都为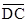
，
∴∠DAC=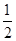∠COD=35°．
故选B
∵∠BAC与∠BOC所对的弧都为
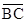，∠BAC=20°，∴∠BOC=2∠BAC=40°，
∴∠AOC=140°，
又
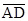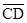=，∴∠COD=∠AOD=
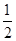∠AOC=70°，∵∠DAC与∠DOC所对的弧都为
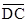，∴∠DAC=
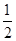∠COD=35°．故选B
练习册系列答案
相关题目
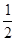，求⊙O的直径．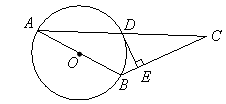
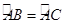； ②
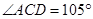； ③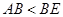
； ④△AEC∽△ACD．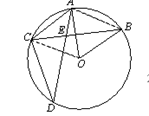
A交圆于E. 
