Question

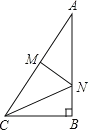
【题目】如图，在Rt△ABC中，∠B=90°，AC=10，BC=6，线段AC的垂直平分线MN分别交AC、AB于M、N两点，则△BCN的面积是（　　）

A.B.C.D.

Answer 1

【答案】B

【解析】

由勾股定理求出AB，由线段垂直平分线的性质得出AN=CN，由勾股定理得出方程，解方程即可得到AN的长及BN的长，进而得到△BCN的面积．

解：∵∠B=90°，AC=10，BC=6，

∴AB===8．

∵线段AC的垂直平分线MN分别交AC、AB于M、N两点，

∴AN=CN，

设AN=CN=x，则BN=8﹣x，

在Rt△BCN中，由勾股定理得：

62+（8﹣x）2=x2，

解得：x=，∴AN=，∴NB=8﹣=，

∴△BCN的面积=BN×BC=××6=．

故选：B．