题目内容
【题目】作图与探究:
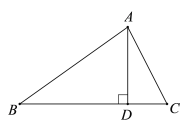
如图,△ABC中,AB=AC.

(1)作图:①画线段BC的垂直平分线l,设l与BC边交于点H;
②在射线HA上画点D,使AD=AB,连接BD. (不写作法,保留作图痕迹)
(2)探究:∠D与∠C有怎样的数量关系? 并证明你的结论.
【答案】(1)①画垂直平分线见解析;②画点D见解析;(2)∠C+2∠D=90°. 证明见解析.
【解析】
(1)①根据以点B和点C为圆心,以大于BC的一半为半径画弧,过两弧的交点作直线l,则l即为所求;②以点A为圆心,AB长为半径画弧,交射线HA于点D,点D为所求;
(2)由AB=AC=AD,则∠ABC=∠C,∠ABD=∠D,利用余角的性质,即可得到2∠D+∠C=90°.
解:(1)①如图所示,直线l为所求;
②如图所示,点D为所求;

(2)由(1)可知,直线l为BC的垂直平分线,
∴AB=AC,
∴∠ABC=∠C,
∵AB=AD,
∴∠ABD=∠D,
∵∠AHB=90°,
∴∠D+∠ABD+∠ABC=90°,
∴2∠D+∠C=90°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目