题目内容
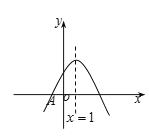
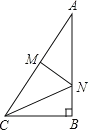
【题目】如图所示,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是对称轴与
是对称轴与![]() 轴的交点.
轴的交点.
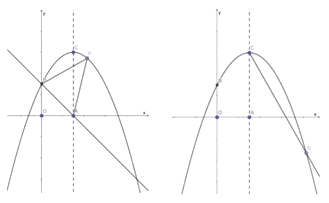
(1)求抛物线的解析式;
(2)如图①所示, ![]() 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求
是抛物线上的一个动点,且位于第一象限,连结BP、AP,求![]() 的面积的最大值;
的面积的最大值;
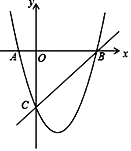
(3)如图②所示,在对称轴![]() 的右侧作
的右侧作![]() 交抛物线于点
交抛物线于点![]() ,求出
,求出![]() 点的坐标;并探究:在
点的坐标;并探究:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 最大值为
最大值为![]() ;(3)存在,
;(3)存在,![]() 点坐标为
点坐标为![]() ,理由见解析
,理由见解析
【解析】
(1)利用待定系数法可求出二次函数的解析式;
(2)求三角形面积的最值,先求出三角形面积的函数式.从图形上看S△PAB=S△BPO+S△APO-S△AOB,设P![]() 求出关于n的函数式,从而求S△PAB的最大值.
求出关于n的函数式,从而求S△PAB的最大值.
(3) 求点D的坐标,设D![]() ,过D做DG垂直于AC于G,构造直角三角形,利用勾股定理或三角函数值来求t的值即得D的坐标;探究在y轴上是否存在点
,过D做DG垂直于AC于G,构造直角三角形,利用勾股定理或三角函数值来求t的值即得D的坐标;探究在y轴上是否存在点![]() ,使
,使![]() ?根据以上条件和结论可知∠CAD=120°,是∠CQD的2倍,联想到同弧所对的圆周角和圆心角,所以以A为圆心,AO长为半径做圆交y轴与点Q,若能求出这样的点,就存在Q点.
?根据以上条件和结论可知∠CAD=120°,是∠CQD的2倍,联想到同弧所对的圆周角和圆心角,所以以A为圆心,AO长为半径做圆交y轴与点Q,若能求出这样的点,就存在Q点.
解:![]() 抛物线顶点为
抛物线顶点为![]()
![]() 可设抛物线解析式为
可设抛物线解析式为![]()
将![]() 代入
代入![]() 得
得
![]()
![]()
![]() 抛物线
抛物线![]() ,即
,即![]()
![]() 连接
连接![]() ,
,
![]()
设![]() 点坐标为
点坐标为![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 最大值为
最大值为![]()
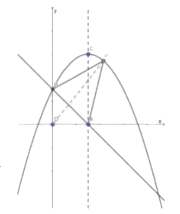
![]() 存在,设点D的坐标为
存在,设点D的坐标为![]()
过![]() 作对称轴的垂线,垂足为
作对称轴的垂线,垂足为![]() ,
,
则![]()
![]()
![]()
在![]() 中有
中有
![]()
![]()
化简得![]()
![]() (舍去),
(舍去),![]()
∴点D(![]() ,-3)
,-3)
![]()
连接![]() ,在
,在![]() 中
中
![]()
![]()
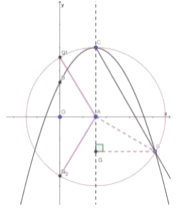
![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆与
为半径的圆与![]() 轴的交点上
轴的交点上
此时![]()
设![]() 点为(0,m), AQ为
点为(0,m), AQ为![]() 的半径
的半径
则AQ=OQ+OA, 6=m+3
即![]()
∴![]()
综上所述,![]() 点坐标为
点坐标为![]()
故存在点Q,且这样的点有两个点.

练习册系列答案
相关题目