题目内容
【题目】如图，AB是⊙O直径，CD为⊙O的切线，C为切点，过A作CD的垂线，垂足为D．
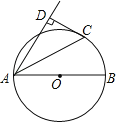
（1）求证：AC平分∠BAD；
（2）若⊙O半径为5，CD＝4，求AD的长．
【答案】（1）详见解析；（2）8；
【解析】
（1）连接OC，则OC⊥CD，因为CD⊥AD从而OC∥AD，利用平行线的性质及等边对等角，等量代换即可得到∠DAC＝∠CAO，从而可知AC平分∠BAD
（2）过点O作OE⊥AD于点E，利用勾股定理求出AE，再利用
即可求解.
（1）证明：如图1，连接OC，
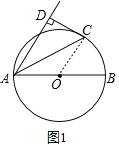
∵直线CD切半圆O于点C，
∴OC⊥CD，
∵CD⊥AD，
∴OC∥AD，
∴∠DAC＝∠ACO，
∵OA＝OC，
∴∠ACO＝∠CAO，
∴∠DAC＝∠CAO，
∴AC平分∠BAD；
（2）如图2，过点O作OE⊥AD于点E，
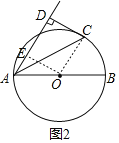
∵∠OCD＝∠OED＝∠CDE＝90°，
∴四边形OEDC是矩形，
∴DC＝OE＝4，
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案【题目】为切实加强中小学生交通安全宣传教育，让学生真正知危险、会避险，郑州市某中学开展了“交通安全进校园”系列活动．为了解七、八年级学生对交通安全知识的掌握情况，对七、八年级学生进行了测试，现从两年级中各随机抽取20名学生的测试成绩（百分制）进行整理、描述和分析（成绩不低于90分为优秀）．
测试成绩（百分制）如下：
七年级：52，78，82，86，77，83，92，87，72，81，93，98，81，69，87，86，80，81，82，94
八年级：87，77，90，79，93，83，88，84，82，94，86，88，57，68，89，59，81，90，88，95
分组整理，描述数据
分组 | 七年级 | 八年级 | ||
画“正”计数 | 频数 | 画“正”计数 | 频数 | |
| 一 | 1 |
| 2 |
| 一 | 1 | 一 | 1 |
|
|
| 2 | |
|
| 正正 | 10 | |
|
| 4 | 正 | 5 |
七、八年级抽取学生的测试成绩统计表
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 82 |
| 81 | 20% |
八年级 | 82.5 | 86.5 |
| 25% |
根据以上信息，回答下列问题：
（1）表中
__________，
__________，
__________，
（2）若该校七年级270人和八年级280人参加了此次测试，估计参加此次测试成绩优秀的学生人数；
（3）根据以上数据，你认为该校七、八年级哪个年级学生掌握交通安全知识较好？并说明理由？
