Question

【题目】如图，BD是正方形ABCD的对角线，BC=4，边BC在其所在的直线上平移，平移后得到的线段记为PQ，连接PA、QD，并过点Q作QO⊥BD，垂足为O，连接OA、OP．

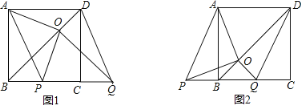
（1）请直接写出线段BC在平移过程中，四边形APQD是什么四边形？

（2）请判断OA、OP之间的数量关系和位置关系，并利用图1加以证明．

（3）在平移变换过程中，设y=S△OPB，BP=x(0≤x≤4)，求y与x之间的函数关系式，并求出y的最大值．

Answer 1

【答案】（1）平行四边形（2）OA＝OP，OA⊥OP，理由见解析（3）当P点在B点右侧时，y＝（x＋2）21；当P点在B点左侧时，y＝（x2）2＋1；当x＝4时，y有最大值为8．

【解析】

（1）根据平移的性质，可得PQ，根据一组对边平行且相等的四边形是平行四边形，可得答案；

（2）根据正方形的性质，平移的性质，可得PQ与AB的关系，根据等腰直角三角形的判定与性质，可得∠PQO，根据全等三角形的判定与性质，可得AO与OP的数量关系，根据余角的性质，可得AO与OP的位置关系；

（3）根据等腰直角三角形的性质，可得OE的长，根据三角形的面积公式，可得二次函数，根据二次函数的性质，可得到答案．

（1）四边形APQD为平行四边形，

理由如下：

∵四边形ABCD是正方形，

∴ADBC，

∵边BC在其所在的直线上平移，平移后得到的线段记为PQ，

∴

∴四边形APQD为平行四边形；

（2）OA＝OP，OA⊥OP，理由如下：

∵四边形ABCD是正方形，

∴AB＝BC＝PQ，∠ABO＝∠OBQ＝45°，

∵OQ⊥BD，

∴∠PQO＝45°，

∴∠ABO＝∠OBQ＝∠PQO＝45°，

∴OB＝OQ，

在△AOB和△OPQ中，

∴△AOB≌△POQ（SAS），

∴OA＝OP，∠AOB＝∠POQ，

∴∠AOP＝∠BOQ＝90°，

∴OA⊥OP；

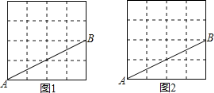
（3）如图，过O作OE⊥BC于E．

①如图1，当P点在B点右侧时，

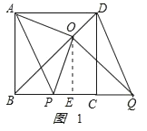
则BQ＝x＋4，OE＝，

∴y＝×x，即y＝（x＋2）21，

又∵0≤x≤4，

∴当x＝4时，y有最大值为8；

②如图2，当P点在B点左侧时，

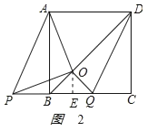
则BQ＝4x，OE＝，

∴y＝×x，即y＝（x2）2＋1，

又∵0≤x≤4，

∴当x＝2时，y有最大值为1；

综上所述，∴当x＝4时，y有最大值为8．