题目内容
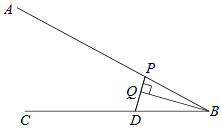
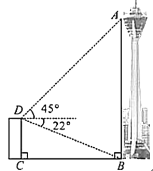
【题目】成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台![]() 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶
处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶![]() 处测得塔
处测得塔![]() 处的仰角为45°,塔底部
处的仰角为45°,塔底部![]() 处的俯角为22°.已知建筑物的高
处的俯角为22°.已知建筑物的高![]() 约为61米,请计算观景台的高
约为61米,请计算观景台的高![]() 的值.
的值.
(结果精确到1米;参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】观景台的高![]() 约为214米.
约为214米.
【解析】
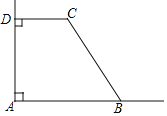
过点D作DM⊥AB于点M,由题意可得四边形DCBM是矩形,由矩形的性质可得BM=CD=61米;在Rt△BDM中,∠BDM=22°,BM=61米,由此可得tan22°=![]() ,即可求得DM=152.5米;再证明△ADM为等腰直角三角形,可得DM=AM=152.5米,由此即可求得观景台的高
,即可求得DM=152.5米;再证明△ADM为等腰直角三角形,可得DM=AM=152.5米,由此即可求得观景台的高![]() 的长.
的长.
过点D作DM⊥AB于点M,由题意可得四边形DCBM是矩形,
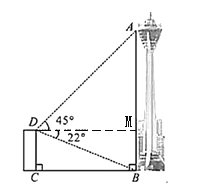
∴BM=CD=61米,
在Rt△BDM中,∠BDM=22°,BM=61米, tan∠BDM=![]() ,
,
∴tan22°=![]() ,
,
解得,DM=152.5米;
∵∠ADM=45°,DM⊥AB,
∴△ADM为等腰直角三角形,
∴DM=AM=152.5米,
∴AB=BM+AM=61+152.5=213.5≈214(米).
答:观景台的高![]() 约为214米.
约为214米.

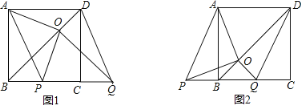
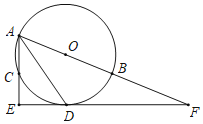
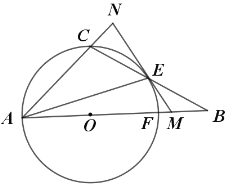
【题目】如图,点D是射线BC上的一定点,点P是线段AB上一动点,连接PD,作BQ垂直PD,交直线PD于点Q.小腾根据学习函数的经验,对线段PB,PD,BQ的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段PB,PD,BQ的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
BP/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PD/cm | 2.00 | 1.22 | 0.98 | 1.56 | 2.43 | 3.38 | 4.35 |
BQ/cm | 0.00 | 0.78 | 1.94 | 1.82 | 1.56 | 1.41 | 1.31 |
在PB,PD,BQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
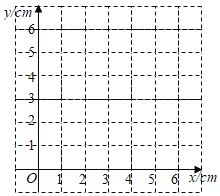
(3)结合函数图象,解决问题:当PD>BQ时,PB长度范围是 cm.