题目内容
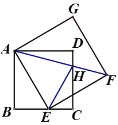
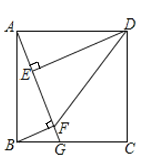
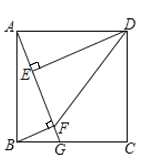
【题目】如图,在正方形![]() 中,
中,![]() ,点G在边
,点G在边![]() 上,连接
上,连接![]() ,作
,作![]() 于点E,
于点E,![]() 于点F,连接
于点F,连接![]() 、
、![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若点G从点B沿![]() 边运动至点C停止,求点E,F所经过的路径与边
边运动至点C停止,求点E,F所经过的路径与边![]() 围成的图形的面积.
围成的图形的面积.
【答案】(1)见解析;(2)见解析;(3)点E,F所经过的路径与边AB所围成图形的面积为4.
【解析】
(1)证明![]() ,根据全等三角形的性质可得出结论;
,根据全等三角形的性质可得出结论;
(2)证明![]() ,根据正方形的性质、相似三角形的性质证明;
,根据正方形的性质、相似三角形的性质证明;
(3)根据所围成的图形是△AOB,求出它的面积即可.
(1)证明:在正方形![]() 中,
中,![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
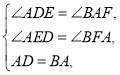
∴![]() .
.
∴![]() .
.
(2)在![]() 和
和![]() 中,
中,![]() .
.
∴![]() .
.
由①可知![]() ,
,
∴![]() .
.
∴![]() .
.
由①可知,![]() ,
,
∴![]() .∴
.∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
(3)∵![]() .
.
∴![]()
∴当点G从点B沿![]() 边运动至点C停止时,点E经过的路径是以
边运动至点C停止时,点E经过的路径是以![]() 为直径,圆心角为90°的圆弧,同理可得点F经过的路径,两弧交于正方形的中心点O.(如图所示)
为直径,圆心角为90°的圆弧,同理可得点F经过的路径,两弧交于正方形的中心点O.(如图所示)
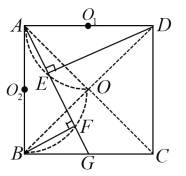
∵![]()
∴所围成图形的面积![]()
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目