题目内容
【题目】如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF.
(1)直接写出点F的坐标:
(2)求线段OB的长及图中阴影部分的面积:
【答案】
(1)
点F(﹣2,0)
(2)
解:过点B作BG⊥x轴于点G,连接OE,OB,则∠AOB=∠EOF=30°,AB=OA=2,∴∠BAG=60°,∴∠ABG=30°,
∴AG=![]() AB=1,BG=
AB=1,BG=![]() =
=![]() ,∴OB=2BG=2
,∴OB=2BG=2![]() ,∵∠BOE=120°,
,∵∠BOE=120°,
∴S扇形=![]() =4π,S菱形OABC=OABG=2
=4π,S菱形OABC=OABG=2![]() ,∴S阴影=S扇形﹣S菱形OABC=4π﹣2
,∴S阴影=S扇形﹣S菱形OABC=4π﹣2![]() .
.
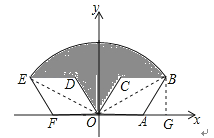
【解析】(1)∵ 菱形OABC的顶点A的坐标为(2,0),∴ OA=2,∵ 将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,∠COA=60°,
∴ ∠AOF=180°,OF=2,即点F在x轴的负半轴上,∴ 点F(﹣2,0)
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半),还要掌握扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2))的相关知识才是答题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目








