题目内容
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
【答案】
(1)解:56÷20%=280(名),
答:这次调查的学生共有280名
(2)解:280×15%=42(名),280﹣42﹣56﹣28﹣70=84(名),
补全条形统计图,如图所示,
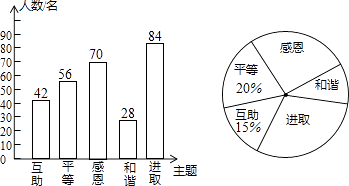
根据题意得:84÷280=30%,360°×30%=108°,
答:“进取”所对应的圆心角是108°
(3)解:由(2)中调查结果知:学生关注最多的两个主题为“进取”和“感恩”用列表法为:
A | B | C | D | E | |
A | (A,B) | (A,C) | (A,D) | (A,E) | |
B | (B,A) | (B,C) | (B,D) | (B,E) | |
C | (C,A) | (C,B) | (C,D) | (C,E) | |
D | (D,A) | (D,B) | (D,C) | (D,E) | |
E | (E,A) | (E,B) | (E,C) | (E,D) |
用树状图为:
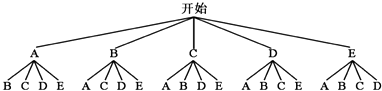
共20种情况,恰好选到“C”和“E”有2种,
∴恰好选到“进取”和“感恩”两个主题的概率是 ![]() .
.
【解析】(1)根据“平等”的人数除以占的百分比得到调查的学生总数即可;(2)求出“互助”与“进取”的学生数,补全条形统计图,求出“进取”占的圆心角度数即可;(3)列表或画树状图得出所有等可能的情况数,找出恰好选到“C”与“E”的情况数,即可求出所求的概率.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图. 
甲组男生训练前、后引体向上个数统计表(单位:个)
甲组 | 男生A | 男生B | 男生C | 男生D | 男生E | 男生F | 平均个数 | 众数 | 中位数 |
训练前 | 4 | 6 | 4 | 3 | 5 | 2 | 4 | b | 4 |
训练后 | 8 | 9 | 6 | 6 | 7 | 6 | a | 6 | c |
(1)根据以上信息,解答下列问题: a= , b= , c=;
(2)甲组训练后引体向上的平均个数比训练前增长了%;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占到该组人数的50%,所以乙组的平均个数不可能提高4个之多.:你同意他的观点吗?说明理由.






