题目内容
【题目】△ABC在平面直角坐标系中的位置如图所示.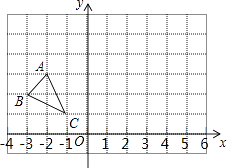
(1)在图中画出△ABC与关于y轴对称的图形△A1B1C1 , 并写出顶点A1、B1、C1的坐标;
(2)若将线段A1C1平移后得到线段A2C2 , 且A2(a,2),C2(﹣2,b),求a+b的值.
【答案】
(1)
解:如图所示:
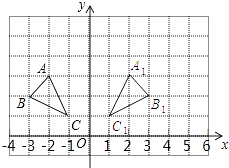
A1(2,3)、B1(3,2)、C1(1,1)
(2)
解:∵A1(2,3)、C1(1,1),A2(a,2),C2(﹣2,b).
∴将线段A1C1向下平移了1个单位,向左平移了3个单位.
∴a=﹣1,b=0.
∴a+b=﹣1+0=﹣1
【解析】(1)根据轴对称的性质确定出点A1、B1、C1的坐标,然后画出图形即可;(2)由点A1、C1的坐标,根据平移与坐标变化的规律可规定出a、b的值,从而可求得a+b的值.
【考点精析】解答此题的关键在于理解作轴对称图形的相关知识,掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线,以及对坐标与图形变化-平移的理解,了解新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.

练习册系列答案
相关题目
【题目】已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
(1)观察表中各对应点坐标的变化,并填空:a= , b= , c=;
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是 .