题目内容
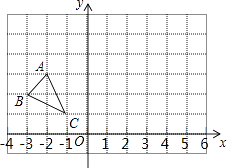
【题目】如图1，在平面直角坐标系中，OA=7，OC=18，将点C先向上平移7个单位，再向左平移4个单位，得到点B，连接AB，BC．
（1）填空：点B的坐标为；
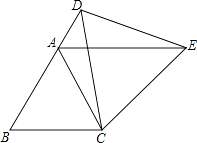
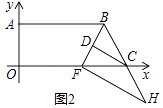
（2）如图2，BF平分∠ABC交x轴于点F，CD平分∠BCO交BF于点D，过点F作FH⊥BF交BC的延长线于点H，试判断DC与FH的位置关系，并说明理由；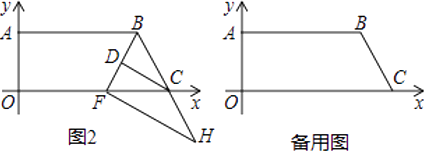
（3）若点P从点C出发以每秒2个单位长度的速度沿CO方向移动，同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动，设移动的时间为t秒（0＜t＜7），四边形OPBA与△OQB的面积分别记为S1，S2，是否存在一段时间，使S1＜2S2？若存在，求出t的取值范围；若不存在，试说明理由．
【答案】
（1）（14,7）
（2）解：结论：PC∥FH．
理由如下：∵BF平分∠ABC
∴∠FBC= 
∠ABC
∵CD平分∠BCO，
∴∠BCD= ∠BCO
依题意得A（0，7），B（14，7），
∴AB⊥y轴，
∴AB∥OC
∴∠ABC+∠BCO=180°
∴∠FBC+∠BCD= ∠ABC+ ∠BCO= （∠ABC+∠BCO）= ×180°=90°，
∴∠BPC=180°﹣（∠FBC+∠BCP）=90°
∴CD⊥BF，
∵FH⊥BF
∴DC∥FH．
（3）解：存在
如图3中，由（1）得B（14，7）
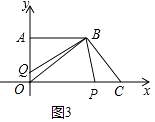
由题意得：PC=2t，OQ=t，则OP=18﹣2t，A（0，7），C（18，0），
S1= （AB+OP）×OA= （14+18﹣2t）×7=﹣7t+112（6分）
S2= t×14=7t（7分）
∵要满足S1＜2S2
∴﹣7t+112＜2×7t（8分）
t＞ 
，
又∵0＜t＜7
∴当 ＜t＜7时，S1＜2S2．
【解析】（1）根据左减上加的平移规则可得B点坐标为（14，7）；（2）平行线间的同旁内角的角平分分线互相垂直，通过转化证得CD与BF垂直；（3）建立关于t的面积表达式，由已知建立不等式，求出t的范围.
【考点精析】解答此题的关键在于理解翻折变换（折叠问题）的相关知识，掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等，以及对坐标与图形变化-平移的理解，了解新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点；连接各组对应点的线段平行且相等．
